Mathematics and Art Workshop
17 Dec. 2014
Domes drawing by Mr. A. Zamani
Geometric Nodes drawing by Ms. S. Vard
Geometry and Tile by Mr. M. Samadieh
Art and Mithal: Reading Geometry as | Geometry and The Interpretation of Meaning: Two Monuments in Iran Carol Bier Research Associate, The Textile Museum | |
This article seeks to develop an interpretation of ornament as geometric pattern that embodies metaphysical intent in Iranian monuments of the fifth/eleventh century. The proposed argument elucidates cultural meaning relevant to a particular time and specific place, with implications for broader application. Reading geometric patterns as visual commentary, this approach relates the presence of patterns in art accompanied by a Qur’anic inscription to both the practice of pattern-making and the contemporary discourse concerning mathematics, philosophy, and the Islamic sciences in Iran. Particular emphasis is placed on the use of a passage from the Qur’an (59:21–24) inscribed on the tomb towers at Kharraqa¯n, in which the Qur’anic term, amtha¯l, is taken literally to refer to the patterns executed on the monuments. | The Alhambra has often served in the West as t he paradigm for understanding geometric pattern in Islamic art. Constructed in Spain in the 13 th century as a highly de fended palace, it is a relatively late manifestation of an Islamic fascination with geometric pattern. Numerous earlier Islamic buildings, from Spain to India, exhibit extensive geometric patterning, which substantiate a mathematical interest in the spatial dimension and its manifold potential for meaning. This paper examines two monuments on the Iranian plateau, dating from the 11 th century of our era, in which more than one hundre d exterior surface areas have received patterns executed in cut brick. Consi dering context, architectural function, and accompanying inscriptions, it is proposed that the geometric patterns carry specific meanings in their group assemblage and combine to form a programmatic cycle of meanings. Perceived as ornamental by Western standards, geometric patterns in Islamic art are often construed as decorative without underlying meanings. The evidence presented in this paper suggests a literal association of geometric pattern with metaphysical concerns. In particular, the argument rests upon an interpretation of the passages excerpted from the Qur’an that inform the patterns of these two buildings, the visual and verbal expression mutually reinforcing one another. Specifically, the range and multiplicity of geometric patterns may be seen to represent the Arabic concept of mithal, usually translated as parable or similitude. The |
Taking Sides, But Who’s Counting ? The DecagonalTomb Tower at Maragha Carol Bier | The Decagonal Tomb Tower at Carol Bier | |
| Abstract : Lu andSteinhardt introduced the term “girih tiles” to describe the set of equilateral polygons that structures a colorful two-dimensional decagonal tiling on the Darb-e Imam in Isfahan, Iran(1453 CE) with distant rootsin the five-fold symmetries articulated in brick on the Gonbad-e Qabud, a tomb towerdated to the late 12 th century CE located at Maragha in western Iran. Their workseeks to establish the early existence of quasi-crystallinetilings long before such means of covering the plane were understood mathematically in the West.Questions remained unanswered as to whether those who constructed thesemonuments were awareof the mathematical significance of their constructions. Lu andSteinhardt, as well as Makovicky and Bonner, who legitimately claimprior discovery of these decagonal tilings and theirsub-grids, all missed the fact that the tower is itself decagonal. This brief paper draws attention to the relationships among architectural form, geometric ornamentation, and Qur’anic inscriptions in assessing the cultural significance of the Gonbad-e Qabud. | Abstract. Of several brick tomb towers constructedat Maragha in western Iran before the Mongol conquests, one in particular, Gonbad-e Qabud (593 H. / 1196-97 C.E.), has generated significant recent attention for its unique patterns with pentagons and decagons. Gonbad-e Qabud is also unusual in havinga decagonal plan. While both plan and decoration distinguishit fromearlier and later towers at Maragha andelsewhere on the Iranian plateau, the ornamentalpatterns follow a long line ofexperimentation with geometric expressions that grace many pre-Mongol buildings in Iran. This article examines in particular the overlappingpolygons and radial symmetries of the tympanum of the cubic Gonbad-e Sork (542 H. / 1148 C.E.) at Maragha, and the pentagonsand squares of the tympanum of the later octagonal tomb tower (486 H. / 1093 C.E.) nearby at Kharraqan. Drawingfrom archival sources (plans, elevations, photographs), analysis ofplane patterns, and comparative architectural data, this article reevaluates the culturalsignificance ofGonbad-eQabud, seeking to situate it within the histories ofmathematics, architecture, andthe arts. |
Geometry in Nature and Persian Architecture
Mehrdad Hejazi
Department of Civil Engineering, Faculty of Engineering, University of Isfahan, Hezar Jerib Street, Isfahan 81744, Iran
Abstract :
Nature displays profound preference for certain specific ratios to design her life-forms. These are geometric relationships that are transcendent and originated from Sacred Geometry. The view that geometry had a ritual origin is a part of a wider view that civilisation itself had a ritual origin, and therefore the history of utilisation of Sacred Geometry by man goes back to many centuries ago. The Pythagorean tradition, and the Egyptian and Babylonian sciences from which it derived, and Persian mathematics, a part of which reflects a Pythagorean intellectuality, are based on the sacred conception of numbers and their symbolism. In the traditional world, geometry was inseparable from the other sciences of the PythagoreanQuadrivium, namely arithmetic (numbers), music and astronomy. Traditional geometry is related to the symbolic configurations of space. Geometric forms such as the triangle, square and various regular polygons, the spiral and the circle are seen in the traditional perspective to be, like traditional numbers, as aspects of the multiplicity of the Unity. Architecture itself has always had a sacred meaning to all traditional civilisations through millennia, by which means man has tried to provide for himself a manifestation of heavens. Persian architecture always emphasised on Beauty, and by means of Sacred
Geometry Persians measured the proportions of heaven and reflected them in the dimensions of buildings on the earth. A comprehensive utilisation of proportions in Persian architecture, such as in the design of plans, elevations, geometric and architectural patterns, and mechanical and structural features, can be proved through geometrical analysis of Persian historical buildings. In this paper, the sacred conception of geometry and its symbolism in the Pythagorean tradition, and Sacred Geometry and proportions in natural life-forms will be explained. The use of the science of geometry in design of a number of Persian historical buildings will be presented. The geometric factors upon which the design of these buildings, from both architectural and structural viewpoints, is made will be discussed.
Introduction to Mathematical Aspects of Art Tile
August 2014
A workshop as an introduction to the mathematical aspects of art and tile work will be held in IMH. Topics in this course included :I
- Drawing with a ruler and math compass
- Tiling by regular polygons
- Tiling Asher
- Tiling and Penn Rose
- Drawing traditional knot
Introduction to the mathematical aspects of the art of tiling was held in August 2014 in three different groups. In this course, participants were introduced to the most important mathematical problems that arise in connection with Art Tile, in five workshops.
Another aspect of this workshop is to create learning experiences related to some mathematical concepts with the help of art tiles and practical tiling using cardboard and foam.
Modularity in Medieval Persian Mosaics
Payam Serji
8 May 2014
Based on the papers of Professor Reza Sarhangi
Math and Art Summer courses and Workshop
23 June-21 September 2013
Math and art group of IMH organized new courses and classes in summer 2013. These classes include math and art concepts. Main topics of the course include :
1. An overview of the basic concepts of art and geometry
2. Adaptability (proportions) on arithmetic and geometric structures
3. Theoretical and Practical Geometry
4. Persian and Western Golden Rectangle
5. Introduction to the Karbandy and styles of drawing it
6. Introduction to and Yazdibandy, Moqarnas and its techniques
7. Introduction to the designs and patterns used in traditional Iranian architecture
8. Methods of drawing of Gereh (a kind of geometric design in iranian tilling) and compare them
9. Brick-working calculations and drawing it
10. Introduction to the Geometric kufic
The program includes classroom course with practical workshop and showing some videos and visit the monuments. Invitation of traditional craftsmen in some meetings is also expected.
One of the main goals of Isfahan Mathematics House is linking Interdisciplinary fields which mathematics is on the one way of this connection. On the other hand, IMH investigates the applications of mathematics in other science.
One of the ideas of mathematics and art group in IMH, is to create this context. So, math and art classes are held in this regards, in an intervals of three months or six months.
In summer math and art classes and workshop were discussed :
- Conception of art from various perspectives
- Introduction to the shapes, volumes and their application in art
- Introduction to the particular relations and proportions the Golden proportions
- Application of Golden proportions in art and architecture
- Introducing Iranian golden proportions
- How to use the knowledge of geometry science in traditional building designs
- Introduction to geometric designs
- Introduction to the types of Gereh (a kind of geometric design in iranian tilling)- and drawing techniques
- How to shape 3d various Volumes
- Workshop of brick-working
- Show some movies about Persian Gereh tiling and Mogharnas
- Introduction to the design Muqarnas
- Teaching karbandi (a type of geometric vault in iranian architecture)
- Teaching Geometric kufic
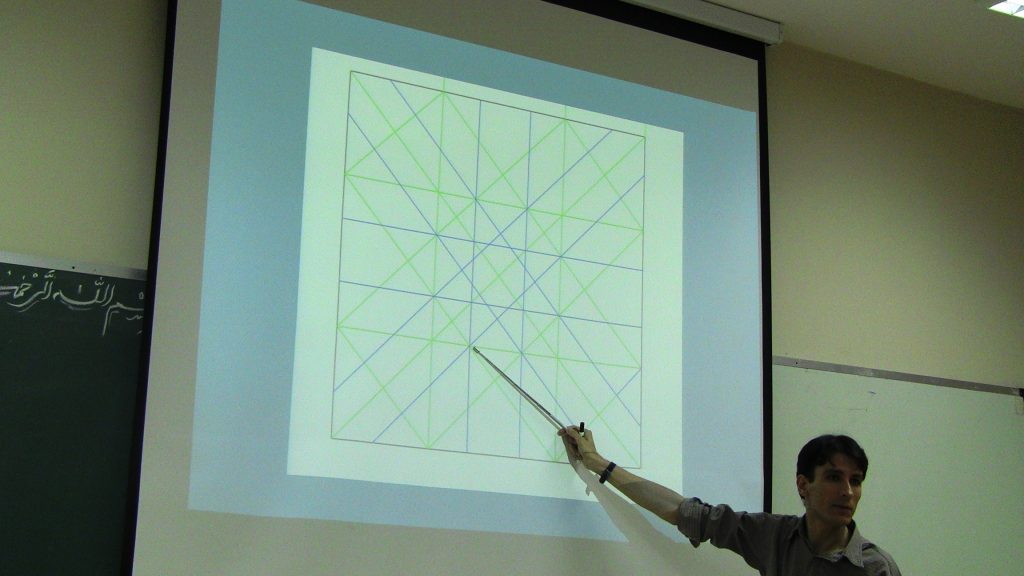
Tiling in the views of Crystallography
Jun 2013
In the following of Mathematics and Art workshop 2013 by IMH and Utrecht Mathematics Department in june 2013, a meeting of mathematics and art experts from different universities was held at IMH. It seems that there are some differences in classification motif and symmetry cases. Fortunately, valuable photos from various tilings in few books gathered by Professor Mahmoud Maheronnaghsh that deals with the classification and symmetry motif is a valuable reference source. So It is necessary to review the following topics in cooperation with tile teachers, physics and mathematics workers :
- Symmetries in tiling is describe by process of Crystallograph as much as possible and for cases that there is no compliance, compatible methods of crystallography be provided.
- Meanwhile resolving differences descriptions by tile experts, a suitable book for teaching forms and symmetry in the tiling is developed.
- Describe a geometric motif, study the difference between theoretical and experimental geometry experts.
- Describe rotational and transfer symmetry mathematically in spherical surfaces that there is application in crystallography.
- And finally after much discussion and reviews, they concluded that there must be a special attention to relationship between empirical and theoretical mathematics for tile, standardization of empirical tiling (mathematically), determine and introduce types of symmetries used in tile, using tiling in teaching geometry, drawing and make it economical for tile working to the public
Suggestions to Isfahan Municipality :
- Useing tile in signs of streets and even houses in this historical city, Center of Persian and Islamic tiling.
- Using tile in municipality buildings.
The Other proposed programs is preparation a pamphlet to introduced relationship between geometry and tile in order to revive reasoning by geometry in education systems.(The Netherlands Freudental Institute communicative with IMH and understanding Islamic architecture, used designs of Isfahan monuments in some Dutch textbooks)
Mathematics and Art Workshop
Isfahan Mathematics House
And
Utrecht Mathematics Department
May 8-10, 2013
Spring Program of Mathematics and Art Workshops
Lecture and workshop Abstracts
Contact information :
0098-3116692013
art.math20013@yahoo.com
art.math2013@mathhouse.org
With Prizing the Team Winners of Ile-de-France Branch of
“APMEP2012 Competition “Mathematics and Architecture” May 2012
About APMEP
The Mathematics and Art workshop was held in Isfahan Mathematics House in 24 May 2012. This one day workshop included 8 lectures and workshops as follows:
Lecturer(s) | Topic |
Mohammad Hossein Eslam-panah | Greh in Greh or Inflation |
Behzad Bagheri | Geometric Origami |
Akbar Zamani | Drawing Arc and Dome |
Sara Abdellahi | Geometry of Islamic Designs |
Narges Assarzadegan | Drawing Geometrical Patterns Using Geometer’s Sketchpad Software |
Meghdad Ghari | Symmetry in Nature and Art |
Mohammad Taghi Ghanbari, Mojtaba Zeraati, Ahmad Azari | Diaphoretic Tiling Workshop |
Nima Valibeigy | The Role of Mathematical Knowledge in Computations Related to Dome Covers in Iran |
A Workshop on an Iranian Astrolabe
A workshop on an Iranian astrolabe was held at Isfahan Mathematics House on Dec 29, 2007. This workshop was led by Wilfred de Graaf and Eric van Lit, two university students from Utrecht University in the Netherlands.
This workshop was organized in two parts; in the first part a brief history of the astrolabe, its origin and its development through centuries in the Islamic world was presented. Then, some applications of the astrolabe and how to use it were described for the participants. In the second part using an astrolabe, the participants tried to solve some problems themselves.
Math & Art Workshops
16 – 18 May 2006
Organizer : Isfahan Mathematics House
In Cooperation with : Isfahan Art University
Supporters :
- Isfahan Municipality
- ISESCO
- UNESCO
- Iranian History of Sciences Research Center, University of Tehran
Scientific Committee :
- Mohammad Bagheri
- Hossein Pournaderi
- Leily Hatamzadeh
- Ali Rejali
- Mahmood Maheralnaghsh
- Ahmad Montazer
- Behnaz Hashemipour
- Aldine Aaten
- Jeanine Daems
- Remke Kruk
- Tom Goris
- Jasper Lukkezen
- Jan Hogendijk
- Daan VanWell
- Mark Roelands
- Huseyin Sen
- Wilfred deGraaf
- Machiel Kwetters
Executive Committee :
- Monireh AnsariPour
- Amir Fakhri-Shooshtari
- Fatemeh Hani Tabaee Zavareh
- Leily Hatamzadeh
- Foroozan KheradPazhuh
- Ali Rejali
- Reza VatanKhah
In Cooperation with: Mehmandar Company
Supporter: IranGate Network
Workshop 1: Tiling regular polygons by means of triangles
Jasper Lukkezen, Michiel Kwetters, Aldine Aaten
In this workshop we used non-traditional ways to tile regular polygons with coloured triangles of different types. Thus we obtained beautiful non-periodic tiling of the plane, which could be indefinitely extended inward and outward. These new tiling resemble traditional Islamic tiling. We began with a short introduction to the basic mathematical ideas which were necessary. Then continued with an interactive part in which the participants were guided and encouraged to design and create their own patterns.
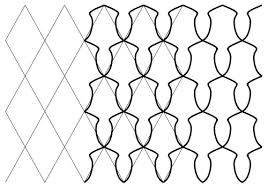
Workshop 2 : Escher Methods on Iranian Tiling
Huseyin Sen, Wilfred de Graaf, Sjoerd Boersma
M.C. Escher (1898-1972 CE) was a famous Dutch artist who created many patterns based on regular division of the plane. His fascination for the subject began with his visit to the Islamic Alhambra Palace in Granada (Spain), where he was astonished by the great wealth of decoration, and the dignity and simple beauty of the whole place. The total absence of any human or animal form in the Alhambra inspired him to create new patterns based on regular divisions of the plane but using alternative forms. Contrary to the Alhambra tiling, which are based on regular polygons with 3, 4, 6 and 12 angles and many Iranian tiling are based on regular polygons with 5, 7 and 10 angles. The aim of this workshop was to apply Escher’s methodology to Iranian tiling. We began with a brief introduction to the methods of Escher and then the participants were guided to use Escher’s methods to design and create new patterns on the basis of Iranian tiling.
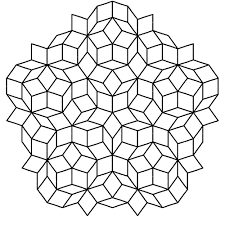
Workshop 3: Penrose Tiling
Daan van Well, Mark Roelands
A tiling of the plane is called periodic if translation symmetry exists in at least two non-parallel directions. If this is not the case, the tiling is said to be aperiodic. A set of tiles is considered aperiodic if the tiles can fill the plane, but not in a periodic way. For a long time it was believed that no such sets exist. In 1973 and 1974, Roger Penrose discovered three sets of tiles which can fill the plane only in an aperiodic way. One set had six tiles and two sets had only two tiles; the shape of some of these tiles is related to Islamic tiling. The first part of the workshop was a basic introduction to the two latter types of aperiodic tiling. In the second interactive part of the workshop, the students had the opportunity to experiment with these two aperiodic sets of tiles. They learned to create some amazing mosaics of a non-periodic character.
Workshop 4: Knot
Maheronaghash, Montazer
Applying different designs on different grids.
Use of Isfahan Architecture in Dutch Books
Emam and Jame Mosque in Isfahan are the most characteristic of Iranian and Islamic architecture and also are world famous architectural wonders. It is hard to found people that have never heard about Isfahan.
But it is interesting that monuments of Isfahan scattered around the world in the form of posters, postcards, So that this monuments used as a learning tool of geometry and math in school textbooks as in Netherlands. Since the architecture, tile and decorative arts of monuments are made based on mathematics, the images imported to Dutch school books as learning examples.
Geometric Patterns in Islamic Art
11-15 Sep 2006
From 11 Sep 2006 through 15 Sep 2006, there is a workshop in Leiden University, the Netherlands, about Geometric Patterns in Islamic Art. Let me write a bit of background how this workshop came to existence. In spring 2006, the Seminar on History of Mathematics in Iran (Persia) was organized at the Department of Mathematics of the University of Leiden (Netherlands) by Dr. Jan P. Hogendijk (one of the coordinators of the current workshop). In that seminar, Jan Hogendijk also conducted a series of optional short classes on the Persian and Arabic alphabet and on Qur’an recitation.
In this workshop, Mr. M. Maheronnaghsh, Mr. A. Montazeri, Mr. A. Bagheri, Ms. Hashemi, Mr. A. Zamani and Mr. A. Rejali were attendend. An exhibition of Mr. Maheronnaghsh works was held.
Scientific Organizing Committee:
Mohammad Bagheri (Tehran, Iran)
Jan Hogendijk (Utrecht and Leiden, Netherlands)
Remke Kruk (Leiden, Netherlands)
Geometric patterns are a prevailing motive in Islamic art and material culture. They are found in Islamic architecture as well as metal work, miniatures, book decoration and textiles for daily use.
Geometric ornamentation in Islamic architecture includes two-dimensional (mosaic) patterns on flat and curved surfaces, and three-dimensional so-called muqarnas-structures, mostly in the interior of domes. Most of the famous patterns in the Alhambra in Granada are based on squares, octagons, equilateral triangles and hexagons. In the Eastern Islamic world, especially in Iran, one often finds more complicated patterns based on pentagons, decagons, and even heptagons and nonagons. There is still a living tradition in Islamic geometric design that inspires modern artists.
The traditional Islamic patterns are witnesses of a highly developed artistic and scientific culture about which little is known today. Much of the history of this whole tradition is unclear and undocumented. The geometric aspects of Islamic architecture have hitherto been studied in vastly different ways by researchers with a variety of backgrounds, including but not limited to: specialists in Islamic culture and history, historians of art and architecture, historians of science, and mathematicians. There has not been much interaction between these groups, although each of them could benefit from all others.
The aim of the proposed workshop is to bring together scholars of these different backgrounds in order to study the geometric aspects of medieval Islamic art and material culture in an interdisciplinary way and to develop modes of cooperation. We hope to open the eyes of the speakers and participants to the many different branches of Islamic art and material culture where geometric design plays a dominant role, and to gain insight into the traditions in which these patterns are created, At the same time, we hope to reduce, for example, math anxiety among specialists of Islamic culture; ignorance of the importance of cultural contexts among mathematicians, etc. To connect to the living tradition, artists will also be involved.
Much attention will be paid to the Iranian tradition. The workshop will be organized in intensive cooperation with the House of Mathematics (www.mathhouse.org) in Isfahan, where a follow-up conference about Mathematics and Iranian-Islamic Architecture will take place in August 2007.
The following interrelated questions are among the ones which will be studied in the present workshop:
1 How were the geometric patterns designed and constructed, what kind of mathematical expertise was used, if any, and what are the surviving textual sources (Arabic and Persian manuscripts, diagrams, etc.)?
2 To what extent were the designers and decorators organized? To what extent was their knowledge documented, and what was the role of oral transmission?
3 What can and should be done in order to document the surviving tradition of Islamic geometric design?
4 What scholarship on traditional geometric design is available in the modern Islamic world?
5 Can modern mathematical concepts (such as crystallographic groups) be helpful to describe and classify the geometric patterns and decorations, and/or to give insight in their historical development? If so, how can such a mathematical methodology be communicated so that it can become a useful tool in the hands of specialists in Islamic culture and art-historians?
6 How can mathematical descriptions and analyses be employed in architectural reconstructions (for example, in the reconstruction of destroyed three-dimensional muqarnas from surviving two-dimensional diagrams)?
During the workshop, attention can also be paid to the design of new artistic patterns of the same types as the traditional medieval Iranian ones.
The workshop can include discussions on the symbolic meanings of geometric ornamentation in Islamic art and material culture, but only on the basis of concrete and authentic medieval textual documents.
The workshop will consist of a general interdisciplinary part (September 11 – 13) and a continuation (Sept. 14-15), which emphasizes mathematical and possibly educational aspects.
