دوره‌ی هندسه‌ی علمی و عملی

مؤلفان: فضل الله رضا، محمود خاتون آبادی، منصور معتمدی

هندسه یکی از برجسته‌ترین آثار فکر انسانی است که در طول دو هزار سال مردان و دانشمندان ما به کمک آن، منطق صریح و روش استدلالی آموخته و نیروی دماغی خویش را برای مطالعه‌ی سایر علوم آماده ساخته‌اند. هندسه موجب درستی و استقامت فکر و مصون بودن از خطاهاست و آن‌ها که هندسه بیاموزند به خوبی می‌توانند در مسائل علمی و عقلی غور کرده، به حوادث و وقایع خارجی بی اعتنا باشند. از لحاظ زندگانی اجتماعی بشر نیز هندسه فوق العاده مورد اهمیت است، چنان که کپلر می‌گوید “بشر برای دانستن، محتاج به اندازه گرفتن است” و اندازه گرفتن کاری است که به کمک حساب و هندسه انجام می‌یابد.

نسبت طلائی و اعداد فیبوناتچی
تالیف: ریچارد اِ. دان­لپ
ترجمه: دکتر منصور معتمدی
کاربرد­های متعدد نسبت طلایی و اعداد فیبوناچی پهنه­‌ای را به وسعت توصیف رشد گیاهان و ساختار بلوری اجسام تا بسط الگوریتم رایانه‌­ای در فرایند جستجوی پایگاه داده­‌ها در­بر می‌گیرد. اگرچه مطالب فراوانی درباره این اعداد نوشته شده است، اما کتاب حاضر با این امید که بتواند شکاف بین منابعی با رهیافت‌­های فلسفی و حتی استعاره­ای و متون ریاضیات صوری را پر کند، نگاشته شده است. کوشیده‌­ام که نه تنها بر خواص اساسی این اعداد تأکید کنم، بلکه اربرد آن­ها را در زمینه­‌های گوناگون ریاضیات، علوم رایانه، فیزیک و زیست‌شناسی نیز نشان دهم. معتقدم این نخستین کتابی است که پس از کشف نارساناها و شبه­‌بلورها در دهه­‌های هفتاد و هشتاد و کاربردهای مستلزم نسبت طلایی در آن­ها، چنین رهیافتی را برگزیده است…

قبله­ یابی در اسلام
تألیف: دیوید ا.کینگ
ترجمه:حسین ناهید
چاپ اول، 1384
« مراعات سمت مقدس ( قبله ) در جهت خانه کعبه، یکی از متمایز­ترین جنبه‌­های اعمال شعائر اسلامی است. تعیین قبله مسئله­‌ا‌ی بود که قرن­‌ها در مرکز توجه و علاقه علمای شریعت اسلامی ( فقها ) و نیز دانشمندان مسلمان قرار داشت. رعایت سمت قبله البته تا زمان حاضر همچنان واجد اهمیت شایان برای صدها میلیون مسلمان است.»
نقل از بخش 1
کتابی که از نظر خواننده محترم می‌­گذرد، ترجمه فصل دوم با عنوان « تعیین سمت مقدس در اسلام» اثر دایرة­المعارفی مؤلف مشهور معارف و آثار تمدن اسلامی به­‌ویژه در زمینه نجوم و افزار نجومی، پروفسور دیوید ا.کینگ تحت عنوان « نقشه­‌های جهانی برای یافتن سمت و فاصله تا مکه » است که با توجه به ارزش علمی _ تاریخی آن از یک سو و اهمیت اطلاع­ یافتن مسلمانان فارسی زبان از چگونگی تحولات و پیشرفت در مسئله عملی قبله­‌یابی از سوی دیگر، مورد نظر شورای علمی خانه ریاضیات اصفهان برای ترجمه به فارسی قرار گرفت. این امر بخصوص با توجه به نقش کلیدی و بسیار عمده­ای که ریاضی­دانان، جغرافی­دانان و افراز­سازان ایرانی به لحاظ علمی و عملی در یافتن راه­ حل­های نبوغ‌­آمیز برای مسئله­‌ای کاملاً بغرنج داشته‌­اند، اهمیت دوچندان پیدا می­‌نماید…

مسابقه­‌های لومونوسف و رگاتا
برگردان: پرویز شهریاری
چاپ اول، 1383
مسابقه‌­های لومونسف سال­‌هاست که در شهر­های مختلف روسیه جریان دارد و بین دانش‌­آموزان دبیرستان ( از سال ششم تا یازدهم ) در رشته‌­های ریاضی، اخترشناسی و دانش زمین، فیزیک، شیمی و ادبیات در مسکو امتحان می‌­شود. این مسابقه‌­ها برای انتخاب کسانی است که در المپیاد جهانی شرکت می‌­کنند و در ضمن برای بالا بردن سطح آگاهی دانش‌­آموزان و انگیزه­ای برای توجه بیشتر به آنچه آموخته‌­اند، نیز می‌­تواند مفید باشد.
در این کتاب مساله­‌های مسابقه‌­ای سال‌های اخیر در زمینه­‌ی ریاضیات آمده است، تنها در یک مورد مساله­‌های مربوط به اخترشناسی و دانش زمین هم، که رابطه‌­ای نزدیکی با ریاضیات دارد، داده شده است تا خوانندگان با نحوه‌­ی پرسش‌­ها و پاسخ‌­ها در این‌باره هم آشنا شوند.

• کسرهای زنجیری حسابی
•  اعداد صحیحی که جذر آنها مقدار حد کسرهای زنجیری متناوب با دوره گردش فرد است.
• متمم قضیه اویلر در کسرهای زنجیری متناوب
• حل معادلات سیاله دو مجهولی درجه اولو دوم به کمک کسرهای زنجیری و …

تحفه الاجله در شناخت قبله

علامه آيه الله حيدرقلي سردار كابلي (قدس سره)
ترجمه مهدي سرابي
چاپ اول،‌1389

تفکر ریاضی
آقای پیام سراجی
آقای مقداد قاری
لوح فشرده اول : اعداد

لوح فشرده آموزشی تفکّر ریاضی که توسط خانه ریاضیات و به همت و کوشش آقای پیام سراجی آماده شده‌ است، مورد تقدیر سازمان پژوهش و برنامه‌ریزی آموزشی وزارت آموزش و پرورش قرار گرفت. در این لوح از طریق برنامه‌های محاسباتی و تعاملی و تصاویر متحرک به مباحث مربوط به اعداد حقیقی، اعداد طبیعی، مفهوم بی‌نهایت، اعداد اوّل، استقرای ریاضی و اعداد نپر و عدد پی پرداخته شده‌ است. تقدیر نامه مذکور را در این لینک ببینید

نرم افزار کبری (Cabri Geometry)

نرم افزار کبری برای آموزش هندسه به دانش آموزان دبیرستانی طراحی شده است. این نرم افزار که در برگیرنده مطالب کتاب درسی و ده‌ها مسئله و پروژه اضافی است، راهنمای فارسی نیز می‌باشد.

نرم افزار کبری (Cabri for mathematics‌) :

کبری یک نرم افزار ریاضی پرکاربرد است. امکانات فوق‌العاده و سادگی کار با نرم افزار از جمله مزیت‌های قابل ذکر آن است. از مزایای دیگر این نرم افزار رسم هر گونه شکل هندسی، نامگذاری، رنگ آمیزی، یافتن معادلات منحنی، رسم منحنی توابع و غیره است. در خانه ریاضیات اصفهان، همزمان با فعالیت بخش دانش آموزی دوره راهنمایی (سال 1387)، آموزش کبری در مدت 2 تا 3 کارگاه یک و نیم ساعتی توسط مدرس مربوط برای دانش آموزان تدریس گردید. همچنین این نرم افزار در دوره ICDL معلمان که در سال 1390 در خانه ریاضیات اصفهان برگزار شد، توسط مدرس مجرب خانه ریاضیات اصفهان به معلمان گرانقدر آموزش داده شد.
معرفی نرم افزار، آشنایی کامل با جعبه و نوار ابزارها، حل مسئله و انجام نمونه‌های بی‌نظیر هنری در دوره‌های این کارگاه باعث شد تا دانش پژوهان ارتباط خوبی با این نرم افزار برقرار نمایند.  خانه ریاضیات آمادگی دارد تا علاقمندان به یادگیری این نرم افزار را راهنمایی نماید.

شهر ریاضیات

این لوح فشرده شامل مجموعه‌ای از مفاهیم پایه علوم ریاضی است که با طراحی زیبا و کاربری آسان امکانی خوب برای افزایش آگاهی علاقمندان در زمینه­‌های مختلف ریاضی را فراهم می­‌کند.

جادوی مقرنس Magic of Muqarnas
دکتر ایوونه دولد سمپلونیوس
مترجم : محمد باقری

این ویدئو، جادوی مقرنس، معرفی نوعی تزیین به نام مقرنس است که در معماری اسلامی، به فراوانی به کار رفته است. مقرنس نامی عربی است برای طاق‌های استالاکتیک مانند، که عبارتند از تزیینات معماری سه بعدی متشکل از اعضای حفره مانندی که در چندین لایه قرار می‌گیرند.مقرنس در حوالی قرن چهارم چجری در شمال شرقی ایران و تقریباً همزمان با آن، و ظاهراً به طور مستقل، در میانه شمال آفریقا پدید آمد، از قرن پنجم هجری به این سو، مقرنس ذر سراسر جهان اسلام گسترش یافت و همانند نقوش گل و کتیبه نویسی، به صورتی‌که از عناصر ویژه معماری درآمد.

قبه‌ای برای کاشانی  Qubba for al-Kashi
دکتر ایوونه دولد سمپلونیوس
مترجم : محمد باقری

جمشید کاشانی ( در گذشته 832 هجری قمری ) یکی از بزرگترین دانشمندان ایرانی است. یکی از ابداعات او عرضه 5 روش برای طراحی طاق‌ها، ازجها و گنبدها تنها با استفاده از خط کش و پرگار است. این لوح فشرده حاوی یک فیلم 16 دقیقه‌ای است که این طرح‌ها را برای 5 نوع طاق مختلف بیان می‌کند. این طاق‌ها می‌توانند طرح دروازه یا پنجره باشند یا با چرخش آنها یک محور گنبد ایجاد شود.

ترسیم‌های ریاضی به کمک پویانمایی رایانه‌ای به روشنی تشریح شده‌اند و با عکس‌هایی از گنبدهای موجوددر سمرقند و بخارا، که کاشانی در آنجا کار می‌کرد، مقایسه شده‌اند. از این ترسیم‌ها برای ساختن نمونه رایانه‌ای از یک قبه یا آرامگاه، به افتخار جمشید کاشانی استفاده شده است. علاوه بر این، در این فیلم باسازی رایانه‌ای رصدخانه‌ای که جمشید کاشانی یکی از بنیان گذارانش بود، دیده می‌شود.

هندسه‌آموز 1

یادداشت استاد محترم جناب آقای فروزان خردپژوه
مدیر سابق خانه ریاضیات اصفهان

یکی از کمبودهای آموزش، به ویژه در دوره های آموزش عمومی (یعنی دوره هایی ابتدایی و راهنمایی تحصیلی)، عدم ارائه ملموس مفاهیم مناسب ریاضی است. از آنجا که دانش آموز شهودی نسبت به مطالب ندارد، ناچار بایستی آن مفاهیم غیر ملموس را حفظ نماید. دانش‌آموزان در این سنین، با توجه به رشد ذهنی خود، می‌توانند در بعضی سطوح نتیجه گیری‌های منطقی نمایند.
با استفاده از ابزارهای آموزشی مناسب می‌توان شهود را در یاد گیرنده افزایش داد. در این صورت او می‌تواند از مفاهیم اولیه‌اش نتیجه گیری‌های خاص خود را داشته باشد. به این ترتیب با کمک ابزارهای آموزشی مناسب می‌توان فکر کردن روی اداراکات را جایگزین حفظ کردن مفاهیم غیر ملموس نمود.
پروژه هندسه آموز (مقدمه) یکی از راهکارهای رسیدن به این هدف است.
ارتباط کودکان با هندسه آموز با دست ورزی با آن به عنوان یک بازیچه آغاز می‌گردد، اما بر والدین و مربیان فرض است که با راهنمایی‌های مناسب خود ذهنیت کودکان را برای آشنایی و درک مفاهیمی که در زیر پوسته آن نهفته است، آماده نمایند. خانه ریاضیات اصفهان با حمایت از گروه‌های کاری علاقه‌مند به فعالیت در زمینه، در پی تدوین چنین راهنمایی‌هایی است.
خانه ریاضیات اصفهان در چهار چوب رسالت‌ها و اهداف خود برای عمومی کردن ریاضیات با پذیرش و حمایت از این نوع نوآوری‌ها امیدوار است تلاش‍‌های مشترک در آموزش بهتر ریاضیات توسعه یابد.

بازی آموزشی هندسه آموزشی هندسه آموز(1) از 24 هرم چهار وجهی همانند تشکیل شده است. پسوند (1) در نام آن موید همین یگانگی هرم‌ها است.این هرم ها داری ویژگی‌های جالبی است.

با کنار هم قرار دادن وجوه مختلف آنها می‌توان اشکال هندسی مسطح مختلفی همچون انواع مثلث، مربع، انواع مستطیل، انواع متوازی الاضلاع، لوزی و چند ضلعی های دیگر و احجام مختلفی همچون مکعب، انواع مکعب مستطیل، منشورهای قائم و مایل با قواعد مختلف و انواع مختلفی از چند وجهی‌های محدب و غیر محدب را ساخت و حجم آنها را محاسبه کرد. هر شکل غیر متقارنی که با این هرم‌ها ساخته شود قرینه آن را و یا مشابه آن را با هر نسبت گویا هم می‌توان ساخت.
بعلاوه همه این‌ها، در نظر بگیریم که اولاً : این هرم‌ها می‌توان در رنگ‌های مختلف تهیه نمود و ثانیاً در یک مجموعه از آنها می‌توان تعدادی را بهم چسپاند، آنگاه کاریی هندسه آمور(1) آشکار می گردد.

اهداف آموزشی

بازی‌های فکری و آموزشی از یک‌سو به دلیل داشتن خصلت تفننی برای والدین، و از سوی دیگر داشتن جنبه آموزشی برای کودکان می‌تواند گزینه جذاب و مناسبی برای هر دو گروه باشد و به خوبی می‌تواند قسمتی از اوقات مشترک والدین و کودکانش را ثمر بخش تر و پربارتر نماید.
از این هندسه آموز (1) یکی از گزینه‌هایی‌ است که برای سال‌ها بخوبی می‌تواند مورد استفاده قرار گیرد و توسط آن بازی‌های جدیدی (با توجه به رشد ذهنی کودکان) مطرح گردد.
این وسیله کمک آموزی دارای اهداف آموزشی زیر است و برای رده های سنی زیر اهداف مختلفی را در بر دارد.

الف- مطالب عمومی
1- تقویت هماهنگی بین مغز و عضلات کوچک دست و چشم کودک.
2- تقویت قدرت بیان کودک
3- تقویت درک منطقی، قدرت استدلال و توانایی حل مساله.
4- ارتقاء درک شهودی از فضای سه بعدی .
5- آموزش نام رنگ ها.
ب- مطالب ریاضی مربوط به دوره اول دبستان
1- ریاضی ماه مهر اول ابتدایی(آموزش نمام برنامه مصوب فقط با بازی).
2- دسته بندی، تناظر یک به یک ، مفهوم اعداد طبیعی، شمارش، جمع و تفریق
3- مفاهیم مختلف هندسی(نقطه،راس،خط،ضلع،سطح،حجم،و..)
4- اشکال مختلف هندسی (مثلث، مربع، مستطیل، لوزی، متوازی الاضلاع،ذوزنقه، و ..)
5- تقارن ها.

ب- مطالب ریاضی مربوط به سال های آخر دبستان
1- نمایش های مختلف و متنوعی برای کسرهای متعارفی.
2- نمایش شهودی جمع و تفریق کسرهای متعارفی.
3- محاسبات سطح و حجم و تدریس احجام و اشکال مختلف هندسی.
4- تقارن ها.

ت- مطابل ریاضی مربوط به دوره راهنمایی
1- آموزش مجموعه ها.
2- آموزش اعداد اول.
3- کسرهای متعارفی.
4-محاسبات حجم و سطح اشکال و احجام هندسی.
5- قضیه فیثاغورس.
6- تشابه.
7-تقارن ها.
8-تقویت محاسبات عددی.

ث- مطالب ریاضی دبیرستانی
1- نمایش شهودی و توجیه هندسی همه اتحاد های جبری دبیرستان.
2-آزمایشگاه برای درس هندسه(1) سال دوم دبیرستان(شامل:تشابه، قضیه فیثاغورس، واحجام مختلف)
3- نمایش شهودی برای برخی دنباله ها و سیرهای عدددی، و فرمول ها(مجموع اعداد فرد متوالی، مجموع مکعبات اعداد طبیعی،فرمول اولر و …)
4-نمایش همه تقارن های موجود در طبیعت بیجان.
5- امکان طرح مسایل متنوعی از نظریه اعداد و ریاضیات گسسته(به ویژه امکان طراحی مجموعه گسترده ای از مسایل باز پاسخ) را در اختیار دبیران قرار می دهد.

ج- برای رشته های دیگر
1- حجم شناسی برای رشته های مختلف هنر.
2- مدل همه رده های اصلی بلورهای اجسام.
3- مدل نمایشی برای برخی ملکول‌ها.

 هندسه یک قطعه!!

یک قطعه در نظر بگیرید : 

اگر طول بزرگترین بالش برابر a باشد آیا می توانید به پرسش های زیر پاسخ دهید:

•  طول هر کدام از بقیه یال ها چقدر است؟
•  مساحت هر وجه قطعه چقدر است؟
•  سطح کل جانبی قطعه چقدر است؟
• حجم قطعه چقدر است؟

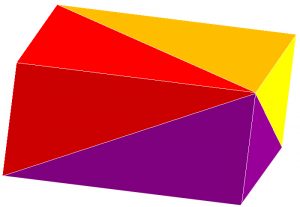
با چند حالت می توان یک مکعب ساخت؟

جعبه از کنار هم چیده شدن چهار مکعب مستطیل کوچک پر می شود.هر کدام از ین مکعب مستطیل ها مطابق شکل های زیر با شش قطعه درست می شوند. ( سه حالت دیگر را در بسته آموزشی می توانید بیابید)  

• آیا می توانید بگوئید صرفنظر از رنگ قطعات چند حالت ممکن است؟

  اگر شرط کنیم که هشت قطعه وجه بالا حتماً از دو رنگ و با تعداد برابر باشند، آنگاه حالت های بیشتری بدست می آید، که برخی از آنها عبارتند از:
      چند حالت امکان پذیر است؟ 

ساخت احجام و محاسبه حجم آنها

با 24 قطعه یک مکعب بسازید:

اگر اندازه ها مانند قبل باشد سطح جانبی ( کل) و حجم مکعب چقدر است؟
— شما می توانید با با 24 قطعه مکعب مستطیل های مختلفی و یا با 12 قطعه شکل های مختلفی بسازید و به پرسش بالا در این حالت پاسخ دهید.

— همه شکل هایی را که تاکنون ساخته اید در نظر بگیرید، تعداد راس های، تعداد یال ها، و تعداد وجه های هر کدام را بشمارید. یا می توانید شکلی هندسی بسازید که در مورد آن جمع تعداد راس ها و وجه ها برابر تعداد یال ها بعلاوه دو نباشد؟

تقارن

دستان چپ و راست ما خیلی به هم شبیه می باشند، مثلاً اگر کف دست راست خود را به آینه بچسپاند، گویی دست چپ خود را کنارش قرار داده اید. دست راست و دست چپ ما با هم فرق دارند، مثلاً دست راست ما در دستکش دست چپ ما جا نمی شود.

در حالی که اگر یکی از قطعات هندسه آموز(1) را به آینه بچسپانید چنین مطلبی پیش نمی آید، بلکه به نظر می رسد که یکی مثل خودش را کنارش قرار داده اید.(امتحان کنید) یعنی هرم های هندسه آموز چپ و راست ندارند.

شاید تصور شود، چون این قطعات چپ و راست ندارند، پس هر شکلی هم با کنار هم قرار دادن آنها ساخته شود چپ و راست نخواهد داشت. اما ین حقیقت ندارد، چرا که با قطعات هندسه آموز می توان اشکل هندسی بسیاری را ساخت که برخی چپ و راست ندارند یعنی متقارن هستند و برخی چپ و راست دارند. به خصوص هر شکلی که با ین قطعات ساخته شود و متقارن نباشد(یعنی چپ و راست داشته باشد)
قرینه آنرا هم با همین قطعات می توان ساخت.
با هشت قطعه می توان دو هرم ساخت که هر کدام گزینه دیگری در آینه باشد.(راهنمایی: برای اینکار اول دو تا دوتا به هم بچسپانید.)
آیا می توانید دو هرم چهار وجهی بسیازید که اولاً هر کدام تصویر دیگری در آینه است و ثانیاً هر دو با قطعاتی مانند هم(هم از نظر شکل و هم از نظر تعداد) ساخته شده اند. اتفاق رخ داده است؟