سمینار و سخنرانی
استفاده از عناصر تاریخی ریاضی در آموزش ابتدایی و متوسطه
سخنران: Konstantinos Nikolantonakis
پنج شنبه 12 اردبیهشت 1397، ساعت 17
تالار میرزاخانی خانه ریاضیات اصفهان
Problem-based Learning
Amir Amirarsalani
University of Hawaii Maui College
شنبه 11 آذرماه 1396، ساعت 18
In this talk, I will present a brief overview of Problem-based Learning (PBL) and discuss the possibility of adopting this method for Science, Technology, Engineering, and Mathematics (STEM) education. We have been recently awarded a National Science Foundation (NSF) grant to implement and examine this approach. Some examples are provided
گفت و شنودهایی پیرامون عبور از حساب به جبر
«منفی» و «منها» در عبور به جبر
دکتر امیرحسین اصغری
یکشنبه 19 شهریور 1396، ساعت 16-17
Alternating sign matrices and tilings
Cédric Boutillier
Université Pierre et Marie Curie
Paris, France
دوشنبه 13 شهریورماه 1396، ساعت 18
Alternating sign matrices are square matrices with entries -1, 0, 1 such that on every row and column, the non zero entries have alternating sign and sum to 1. These matrices appeared naturally when Robbins and Rumsey studied some generalisation of the determinant about 40 years ago. We will review some properties of these matrices, discuss connections with other nice combinatorial objects, such that tilings with dominos or rhombi, the ice model, and present some techniques used in the proof of the enumeration of these
matrices
خوشهبندی بر مبنای مدل و چالشهای آن
دکتر عباس خلیلی، استاد ریاضی دانشگاه مک گیل کانادا
شنبه 10 تیرماه 1396، ساعت 17:30، تالار میرزاخانی
خوشه بندی یک مسئله یادگیری بدون نظارت است که در پنجاه سال اخیر خیلی از متخصصان آمار و آموزش ماشینی را به خود جلب کردهاست. در این سخنرانی یک رویکرد عام بر مبنای مدل برای خوشه بندی بر اساس مدلهای معروف به مدل های آمیخته معرفی میشود. این رویکرد برای مسایل خوشه بندی در کاربردهایی از زیست شناسی و پزشکی تا مهندسی، اقتصاد و علوم اجتماعی به کار میرود.
در قسمت دوم سخنرانی، تعدادی مسایل باز در زمینه استنباط آماری در زمان استفاده از مدلهای آمیخته متناهی در خوشه بندی مطرح میشوند.
Prime numbers, yesterday, today…, an inspiring topic
Jean Marc Deshouillers, Bordeaux University, France
چهارشنبه 7 تیر 1396، ساعت 17:30
Prime numbers (2, 3, 5, 7, 11, 13, 17…), those integers which cannot be written as a product of two integers larger than 1, are the fundamental “bricks” of the multiplicative structure of the integers. Euclide already discovered several of their properties, among other the fact that they cannot be described by a finite collection. In the XVIII th and XIX th centuries, Euler, Riemann and others developed a new analytical approach, which led to a good evaluation of the number of prime numbers up to a given bound, as well as to a deep conjecture which is surely nowadays the most important question in all mathematics, the “Riemann hypothesis”. 1978 saw this field of pure research enter applied science, through the development of powerful cryptography systems. More recently, Ben Green and Terence Tao (who received the Field medal in 2006) showed that prime number nicely behave as regards arithmetic progressions. In 2013, Zhang proved that there can be pairs of prime numbers which can be very close one to the other, where as Helfgott proved that every odd integer larger than 6 is a sum of three primes. The talk aims at introducing those topics to an audience of “amateur” who are not a prior specialized
مربعهای لاتینی متعامد، ساختار مخصوص و موارد استفاده
دکتر هادی خرقانی
استاد ریاضی دانشگاه
Lethbridge, Canada
پنجشنبه، 25 خردادماه 1396، ساعت 17
ابتدا با روش ساده ساختاری همه با هم برای هرعدد اول p نشان میدهیم که درست p -1 مربع (مخصوص) لاتینی متعامد وجود دارد. از این خاصیت استفاده کرده و نشان میدهیم که از وجود دو عدد اول متوالی میتوان جبری ماتریسی ساخت که دارای خواص متمایز و مفیدی است.
استفاده از عناصر تاریخی ریاضی در آموزش ابتدایی و متوسطه
سخنران: Konstantinos Nikolantonakis
پنج شنبه 12 اردبیهشت 1397، ساعت 17
تالار میرزاخانی خانه ریاضیات اصفهان
Abu Rayhan Biruni as an applied scientist
Jan P. Hogendijk، استاد تاریخ ریاضیات دانشگاه اوترخت هلند
دوشنبه 11 اردیبهشت 1396، ساعت 18:30
فایل سخنرانی
Abu Rayhan Bırunı as an applied scientist
http://www.albiruni.nl/
Abu Reihan Biruni (362-440 H/972-1048 CE) was one of the most interesting scholars in the medieval Islamic tradition. We will first discuss his personality and life. He was an expert not only in mathematics, astronomy, and geography but also in languages, literature and history. Then we will try to characterize his work. Biruni possessed an extensive theoretical knowledge but his main interest was in applied science. As an example, will discuss some his contributions in timekeeping including prayer times and the determination of the qibla. Biruni wrote several original works on the astrolabe, an instrument that can be used to solve these problems. We will illustrate our examples by means of drawing from medieval Arabic manuscripts, and will discuss Biruni’s approach to uncertaint and errors in measurements and computations. Finally, we will discuss the availability of Biruni’s works (see our website www.albiruni.nl
The quadrant: a medieval geometric computer
Wilfred de Graaf and Tom Reijngoudt
سهشنبه 12 اردیبهشت 1396، ساعت 18:30
The participants will recieve a slightly modernized model of a quadrant as it was used by Muhammad Ibn Musa Khwarizmi (third century Hijri) and his successors. We will first show how to use the quadrant for the multiplication and divison of a large class of numbers. An important application of the quadrant was the solution of trigonometrical problems without computation. For any given date in the Persian calendar, the participants will use the quadrant to easily determine the maximum height of the sun at noon, the place of sunrise and sunset, and the length of the day. We will also discuss the modern formulas for the solution of these problems. Depending on time, we will propose to the participants to think about possible applications of the quadrant to more difficult problems
مجموعههای بینهایت در ریاضیات
Heike Mildenberger
University of Freiburg, Germany
پنجشنبه 24 فروردینماه 1396، ساعت 18
خانه ریاضیات اصفهان، تالار میرزاخانی
People can think of infinite sets, however, there is no physical experiment that would prove or disprove their existence. About 140 years ago, mathematicians decided to accept an axiom that states that there is an infinite set. An axiom is a plausible assumption that does not have a proof. In the talk we will look at some of the properties of infinite sets in mathematics
ما می توانیم به بی نهایت فکر کنیم ولی هیچ آزمایش فیزیکی وجود یا عدم وجود آنها را اثبات یا رد نمی کند. ریاضیدانان حدود 140 سال پیش تصمیم گرفتند اصولی را در مورد وجود بی نهایت بپذیرند. اصولی که قابل پذیرش به نظر می رسیدند ولی اثباتی برای آنها وجود نداشت. در این سخنرانی ما به بعضی خواص مفهوم و مجموعه های بی نهایت در علوم ریاضی خواهیم پرداخت.
سخنرانی عمومی با موضوع
موازییك چوبی پنروز
دوشنبه 21 فروردین 1396، ساعت 18
Thomas Fernique
تالار میرزاخانی خانه ریاضیات اصفهان

کاشیکاریهای پنروز (Roger Penrose) و طرحهای سنتی ایرانی- اسلامی
دکتر پیام سراجی
دوشنبه 2 اسفند 1395، ساعت 17
تالار میرزاخانی خانه ریاضیات اصفهان
راجر پنروز در دهه 1970 میلادی نوع جدیدی از کاشیکاری ارائه داد که دارای خواصی متفاوت از کاشیکاریهای متداول بود، این کاشیکاریها غیر متناوب بودند، دارای تقارن مرکزی پنجتایی بوده و فقط از چند نوع محدود کاشی ایجاد میشدند. این کشف پنروز هم به دلیل جنبههای زیباییشناسانه آن و هم به دلیل کاربردی که در مطالعه شبه بلورها پیدا کردند، بسیار مورد توجه قرار گرفت. در چند سال اخیر ادعاهایی در مورد ارتباط این کاشیکاری با نوع خاصی از کاشیکاری سنتی ایرانی مطرح شده است.
در این سخنرانی پس از مروری کوتاه بر مقدمات و کارهای انجام شده در این زمینه، یک روش جدید از ایجاد کاشیکاریهای نامتناوب با کمک طرحهای سنتی ایرانی-اسلامی و اثبات ریاضی خواص آن ارائه میشوند.
حکمت و ریاضی
دکتر رسول رکنیزاده، عضو هیئت علمی دانشگاه اصفهان
همزمان با همایش آسیب شناسی و برنامهریزی
پنجشنبه 20 آبان 1395، ساعت 18 الی 19
تالار میرزاخانی، خانه ریاضیات اصفهان
در سالهای اخیر توسط بعضی متفکران موضوع حکمت پژوهی در مقابل دانش پژوهی مطرح شده است. این روش را در مورد یکی از فاخرترین دستاوردها بشری یعنی ریاضی مورد تحلیل قرار میدهیم. در این سخنرانی به بعضی پرسشها در این رابطه پرداخته میشود:
آیا ریاضی از جنس معرفتهای دیگر بشری نظیر علوم طبیعی است؟
در این صورت ریاضی معرفت پیرامون چه نوع واقعیاتی است؟
معیار تشخیص ریاضی مهم از غیر مهم چیست؟
نگاه حکیمانه به ریاضی میتواند به چنین پرسشهایی، پاسخ دهد. درک حکیمانه از ریاضی منجر به برانگیختن شوق یادگیری در متعلمان ریاضی میشود.
یادآوری برخی از نتایج مسائل ریاضی
دکتر امید علی شهنی کرمزاده، دانشگاه شهید چمران اهواز
پنجشنبه 6 آبان 1395، ساعت 17
.
چگونه میتوان تفکر ریاضی را در کلاس درس ترویج داد؟
دوشنبه 15 شهریور 1395، ساعت 17
سخنران: پروفسور فرناندو آرزارلو، دانشگاه تورین- ایتالیا، رییس کمسیون بین المللی آموزش ریاضی
با کمک خداوند و به یاری او، این را بر زبان میآورم که جبر هنر علمی میباشد.
مفعولاتی که این علم با آنها سر و کار دارد اعداد مطلق و کمیتهای قابل اندازهگیری هستند که گرچه خودشان به نوبه خود
نامعلوم میباشند، اما با پدیدههایی در ارتباط میباشند که خود شناخته شدهاند، که به وسیله آنها تعییم مقادیر نامعلوم ممکن و میسر میگردد.
عمر خیام، رسالهای در باب اثبات مسائل جبر
یکی از مسائل بسیار حساس و ظریف در بحث آموزش و یادگیری ریاضیات حصول اطمینان از این نکته است که آیا دانشآموزان ذهنیت لازم برای حصول حس ریاضی در شرایط آموزشی که با آن مواجه میشوند را بدست می آورند: محققینی همچون شونفیلد در مورد به وجود آوردن حس ریاضی صحبت کردهاند.[1]
این موضوع نقطه مقابل تصویری است از تصویری که اغلب مردم نسبت به ریاضیات بهعنوان مجموعهای از قوانین و الگوریتمهایی در ذهن دارند که باید آنها را به ذهن بسپارند تا بتوانند به سؤالاتی جواب دهند که گاهأ از هر حس واقعی نیز به دور میباشند.
در واقع، کلاس درس، محیطی فرهنگی است که در آن فعالیتها و اعمال روزانه مشخص شده و موضوعاتی که در آن آموزش داده میشود معنی پیدا میکنند. بنابراین دانشآموزان، کم و بیش آگاهانه و پیوسته ولی اجتناب ناپذیر، وادار به تبعیت از پروتکلی از قوانین میشوند تا بتوانند پرسشهای معلم را پاسخ دهند. این همان مسیری است که آنها احساس خود به ریاضی را توسعه میدهند. مشکل این جاست که بین آنچه مورد نظر معلم از ریاضیات برای انتقال به دانشآموزانش است و احساسی که دانشآموزانش از ریاضیات بر اساس تجارب و روشهای معلم در این حوزه کسب میکنند، ممکن است تفاوت معنیداری وجود داشته باشند.
در این سخنرانی، نشان خواهم داد چگونه میتوان موقعیتهای یادگیری مناسب را طراحی و شیوههای مختلف کلاس درس را دنبال کرد که بتوان حس اصیل ریاضی را از طریق درهم پیچیدگی حل مسئله، ایجاد کرد. هدف ایجاد تصویری از معلم است که فقط نقش انتقال دهنده قوانین را نداشته باشد، بلکه ترویج کننده حس ریاضی در بین دانشآموزان باشد. روش آموزش/یادگیری پیشنهاد شده به “روش تحقیق متنوع- MVI” که بر پایه روش تنوع [2] و منطق علمی تحقیق که به گالیلی باز میگردد و در ICT کاربرد دارد، معروف است.
توسعه MVI در کلاس درس میتواند به عنوان یک ابزار برای توسعه چشم اندازی مناسب از ریاضیات و پیشدارویی برای جلوگیری از تصور ریاضی به صورت مجموعهای از قوانین و کاربردها، مورد استفاده قرار گیرد. درطول سخنرانی روش MVI با مثالهای ملموس از فعالیتهای کلاس درس ارائه خواهد شد.
1.1Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense-making in mathematics. In D. Grouws (Ed.), Handbook for Research on Mathematics Teaching and Learning (pp. 334-370). New York: MacMillan.I
2.1Marton, F., Runesson, U., & Tsui, A. (2003). The space for learning. In: F. Marton & A. Tsui (Eds.), Classroom discourse and the space for learning, pp. 3- 40. Mahwah, NJ: Lawernece Erlbaum Associates, Inc.I
کاربرد دادههای شبیهسازی شده و پویا نماها در تدریس مفاهیم آماری
شنبه 30 مرداد 1395، ساعت 17 تا 18
تالار میرزا خانی خانه ریاضیات اصفهان، سخنران: آندره بلج
Andrej Blejec ، National Institute of Biology and University of Ljublajana, Slovania
The President of the International Association of Statistical Education
همواره آمار را به عنوان رشتهای از علوم دیده و شناختهایم که وظیفه آن بررسی دادههاست، بدون اینکه توجهی به این داشته باشیم که آنها مربوط به چه بخشی است. ممکن است از صنعت یا کشاورزی، پزشکی، بیمه و یا مسایل روانشناسی باشد. منبع دادهها هرچه که باشد نگرش و برخورد آمار با آنها طبق مفاهیمی است که خود بر پایه اثباتهای قابل پذیرش از طرف جامعه ریاضیدانان استوارند.
حال با دو پرسش اساسی مواجه میشویم که:
۱. چه باید کرد اگر مخاطب این مفاهیم و کاربردها که اغلب در رشتهای غیر از ریاضیات تحصیل کرده و پیش نیاز لازم را ندارد، اثبات ما را نپذیرد و یا نتواند به درک ذهنی مناسبی راجع به قضیه و همچنین اثبات مطرح شده دست یابد؟
۲. از سوی دیگر آیا نیاز است مخاطب، مخصوصاً اگر دانشآموز باشد، قضیهای را کاملاً یاد بگیرد؟ یا اینکه تنها کافی است وی به درک کافی راجع به مفاهیم برسد؟
در این سخنرانی نقش دادههای شبیه سازی شده و همچنین بهرهمندی از پویا نماها برای تفسیر این شبیه سازیها به منظور درک و تدریس مفاهیم و قضایای آماری را بررسی مینماییم.
نخست به بررسی انواع دادهها، مزایا و معایب آنها خواهیم پرداخت، سپس با اهداف آموزش آمار و کمکگیری از دادهها و شبیهسازی برای این کار آشنا میشویم و در ادامه به عنوان مثالهایی کاربردی، دو روش آماری نام آشنا (متدهای کوچکترین مربعات و بزرگترین درست نمایی) که برای تخمین پارامترهای جامعه استفاده میشوند را با استفاده از دادههای شبیه سازی شده و همچنین پویا نماها بررسی میکنیم و در نهایت تعاریفی بنیادین در علم آمار، یعنی جامعه و نمونه را مرور مینماییم و خواهیم دید که تا چه اندازه انتخاب نمونه در شبیهسازیها میتواند ما را به حقیقت جامعه دور یا نزدیک بنماید.
در پایان نشان داده میشود که چگونه مباحث آماری که در زندگی روزمره بارها با آنان مواجه هستیم و دارای اثباتهایی پیچیده با پیش زمینههایی ریاضیوار میباشند، با استفاده از شبیهسازی دادههایی از همین وقایع روزمره و ملموس و تفسیر این دادهها با پویا نماها قابل درک و آموزش به دانشآموزان و دیگر افراد خواهند بود.

کاشیکاریهای پنروز (Roger Penrose) و طرحهای سنتی ایرانی- اسلامی
دکتر پیام سراجی
دوشنبه 2 اسفند 1395، ساعت 17
تالار میرزاخانی خانه ریاضیات اصفهان
راجر پنروز در دهه 1970 میلادی نوع جدیدی از کاشیکاری ارائه داد که دارای خواصی متفاوت از کاشیکاریهای متداول بود، این کاشیکاریها غیر متناوب بودند، دارای تقارن مرکزی پنجتایی بوده و فقط از چند نوع محدود کاشی ایجاد میشدند. این کشف پنروز هم به دلیل جنبههای زیباییشناسانه آن و هم به دلیل کاربردی که در مطالعه شبه بلورها پیدا کردند، بسیار مورد توجه قرار گرفت. در چند سال اخیر ادعاهایی در مورد ارتباط این کاشیکاری با نوع خاصی از کاشیکاری سنتی ایرانی مطرح شده است.
در این سخنرانی پس از مروری کوتاه بر مقدمات و کارهای انجام شده در این زمینه، یک روش جدید از ایجاد کاشیکاریهای نامتناوب با کمک طرحهای سنتی ایرانی-اسلامی و اثبات ریاضی خواص آن ارائه میشوند.
از تحلیل دادهها به علوم دادهها (آشنایی با رشته جدید علوم دادهها و ارتباط آن با آمار)
توسط آقای دکتر عادل محمدپور
دانشیار گروه آمار دانشگاه صنعتی امیرکبیر
چهارشنبه 2 دی 1394
ساعت 14
گفتگویی علمی پیرامون مسایل آموزش ریاضی و برنامهریزی درسی
آقای دکتر احمد فاتحی
استاد بازنشسته دانشگاه ایالتی تگزاس آمریکا
دوشنبه 20 مهر 1394، ساعت 17 تا 18:30

سخنرانی با موضوع حل معماها به عنوان ابزاری برای موفقیت تحصیلی
آقای دکتر حسین شاه محمدی
(استاد ریاضی انستیتو تکنولوژی راچستر نیویورک، آمریکا)
سهشنبه 6 مرداد 1394، ساعت 12-10
در ادامه سخنرانیهای عمومی خانه ریاضیات اصفهان، با کمال خوشوقتی به اطلاع تمام دانشآموزان دبیرستانها و خانوادههای محترم و علاقهمندان میرساند که روز سهشنبه 6 مرداد 1394، ساعت 12-10 یک سخنرانی با عنوان حل معماها به عنوان ابزاری برای موفقیت تحصیلی توسط آقای دکتر حسین شاه محمدی
(استاد ریاضی انستیتو تکنولوژی راچستر نیویورک، آمریکا) در محل خانه ریاضیات اصفهان ارائه مینمایند.
کارگاه سه روزه با عنوان
روشهای انتخاب متغیرها در مسائل رگرسیونی با بعد بالا
30 تیر 1394 الی 1مرداد 1394
ویژه دانشجویان سالهای آخر کارشناسی آمار ، دانشجویان کارشناسیارشد و دکتری سراسر کشور و اعضاء هیئت علمی دانشگاهها
نتایج نظرسنجی
خانه ریاضیات اصفهان کارگاه سه روزهای را برای دانشجویان سالهای آخر کارشناسی آمار، دانشجویان کارشناسیارشد و دکتری سراسر کشور و اعضاء هیئت علمی دانشگاهها ،تحت عنوان زیر برگزار مینماید. بدلیل استقبال زیاد دانشجویان برای شرکت در این کارگاه، مهلت ثبتنام بدون اقامت، تا شنبه 26 تیرماه 1394 تمدید شد.
“روشهای انتخاب متغیرها در مسایل رگرسیونی با بعد بالا“
ارائه دهندگان :
آقای دکتر عباس خلیلی (دانشگاه مک گیل کانادا)
با همکاری آقایان دکتر سروش علیمرادی (دانشگاه صنعتی اصفهان)
و دکتر ایرج کاظمی (دانشگاه اصفهان)
چکیده
Abstract : In recent years, due to the availability of advanced technology, we have witnessed the rise of large scale data, colloquially referred to as big data, in different fields of scientific research, ranging from biology and medicine to engineering, the social sciences and financial econometrics. A common statistical problem of interest in the analysis of such data is to model a response variable of interest as a function of a small subset of a large number of potential features (covariates
موضوعات زیر در این کارگاه مطرح میشوند :
I: Overview of linear, generalized linear regression, and mixture of regressionmodels.I
II: Model selection problem in general, and feature (variable) selection.I
III: New regularization techniques in high or ultra-high dimensional regressionmode



Some researches on tilings in a Persian manuscript in Paris
پروفسور یان پیتر هوخندایک
استاد دانشگاه اترخت هلند
پنجشنبه 31 اردیبهشت 1394، ساعت 9
Abstract : The National Library in Paris preserves a famous manuscript (Or. 169, 180a-199a) devoted to Persian-Islamic tilings. The manuscript was translated into Russian by M. Bulatov (1988), who showed how some of its rectangular diagrams could be transformed into tilings of the whole plane by translation and reflections. In the 1990s, the manuscript was translated into modern Persian by Seyyed Alireza Jadhbi from Tehran, and it was researched extensively by the Turkish architect Alpay Ozdural, who unfortunately died in 2003 before most of his researches had appeared. In some of his published papers, Ozdural studied other ways to cover the plane by tilings composed from diagrams in the manuscript. In the talk we will show some examples. It is hoped that most of the research by Ozdural will be
published in 2015 by an interdisciplinary and international team
Persian mathematics and astronomy in 17th century Holland
پروفسور یان پیتر هوخندایک
استاد دانشگاه اترخت هلند
شنبه 2 خرداد 1394، ساعت17
Abstract : Between 1625 and 1629, the Dutch mathematician and oriental scholar Jacobus Golius (1596-1667) collected a very fine collection of more than 400 Arabic manuscripts in Aleppo and Istanbul, and brought them to the city of Leiden in Holland. We will discuss to what extent these manuscripts were used in 17th-century Holland as sources of knowledge about the contributions of mathematicans and astronomers from greater Iran. To this end we have gathered information from printed works, publications on Leiden university, the Arabic manuscripts themselves, and also from a Latin manuscript by his student and colleague Frans van Schooten junior (1615-1660)
ارتباط کاشیکاری نامتناوب پنرز با طرح های سنتی معماری ایرانی – اسلامی
پیام سراجی
دانشجوی دکترای منطق دانشگاه تبریز
پنجشنبه 31 اردیبهشت 1394، ساعت 10:30 صبح
چکیده : راجر پنرز در دهه 1970 نوع جدیدی از کاشیکاری ارائه داد که خواص آن با کاشی کاریهای شناخته شده تا آن زمان تفاوتهای اساسی داشت. در دهه بعد این کاشیکاریها در بررسی شبه کریستالها به کار رفت و از این جهت مورد توجه فیزیکدانها هم قرار گرفت. در این سخنرانی به بررسی ارتباط این موضوع با طرحهای سنتی معماری ایرانی پرداخته و روش جدیدی برای تبدیل کاشی کاری پنرز به یک کاشی کاری با طرحهای سنتی ارائه میکنیم.


A square law of attraction for strong patterns of Hopfield networks and modeling behavioral prototypes and psychotherapy
پروفسور عباس عدالت
استاد علوم کامپیوتر و ریاضیات دانشکده محاسبات امپریال، کالج لندن
روز شنبه 29 فروردین 1394
ساعت 18-17
: Abstract
Hopfield neural networks, introduced by John Hopfield in 1982, were the first artificial model of associative memory and the precursor of today’s Deep Belief Nets, which have provided a revolution in Machine Learning in recent years. In this talk, I will introduce the notion of strong, i.e., multiply learned, or equivalently, strongly stored patterns in Hopfield networks. I show that strong patterns have a large basin of attraction and that their retrieval capacity, in the presence of simple patterns, rises proportional to the square of their multiplicity or strength. This square law of attraction, which is rigorously proved by solving the mean field equations for the stochastic Hopfield networks, enables us to use strong patterns to model cognitive and behavioral prototypes as well as attachment types in developmental psychology. Psychotherapy of an individual can then be modeled, at its most basic level, as the learning of a new strong pattern whose multiplicity or strength eventually exceeds that of the strong pathological neural pattern learned earlier in life. Finally I will explain how this neural model has motivated the development of a new and integrative psychotherapeutic method, called self-attachment, which in a number of case studies so far has shown to be more effective than current available technique
سری سخنرانیهای وِیژه خانه ریاضیات اصفهان
دوشنبه 6 بهمن 1393
ویژه دانشآموزان، دانشجویان و معلمان
سخنرانی آقای دکتر مجید میرزاوزیری (دانشگاه فردوسی مشهد) ویژه دانشآموزان متوسطه دوم با موضوع شکلهای دو به دو متقاطع
دراین صحبت قصد داریم به ارائه چند ترفند برای طرح مسألههای ریاضی بپردازیم. برای این منظور به مسألههایی با صورتهای متفاوت و حل مشابه و مسألههایی با صورتهای مشابه وحل متفاوت توجه میکنیم.
سخنرانی آقای دکتر مجید میرزاوزیری (دانشگاه فردوسی مشهد)
ویژه معلمان با موضوع جدول نظام دار
یکی از روشهای حل مسألههای شمارشی، استفاده از استقراء ریاضی برای به دست آوردن یک رابطه بازگشتی است که دانشآموزان آن را جدول نظامدار مینامند. در اکثر مواقع، دانشآموزان تفاوت ظریف یک دنباله بازگشتی و سؤالهایی که موسوم به تست هوش هستند را متوجه نمیشوند. قصد داریم با چند مثال این تفاوت را بررسی کنیم.
سخنرانی آقای دکتر امید نقشینه ارجمند (دانشگاه امیركبیر)
ویژه دانشجویان با موضوع از قضیه فیثاغورث تا سریهای فوریه
قضیه فیثاغورث از معروفترین و قدیمیترین قضیههای هندسه مسطحه است و مبحث سریهای فوریه حاکی از این است که یک تابع را چهگونه میتوان با ترکیب خطی چندجملههای مثلثاتی «تقریب» زد. این دو موضوع شاید در نگاه اول چندان مربوط به نظر نرسند ولی در واقع ارتباطی مهم بین این دو وجود دارد. در این سخنرانی در این مورد صحبت خواهد شد و در نهایت به برخی از کاربردهای سریهای فوریه اشاره میشود.
سخنرانی آقای محمد حسن حسینی (مدرس مراکز تربیت معلم و دبیر ریاضی تبریز)
ویژه معلمان ریاضی با موضوع عوامل اصلی ریاضی هراسی چیست و موانع استقبال دانش آموزان از حل مسائل ریاضی کدامند؟
چالشهای صنعت، فرصتهای علوم کامپیوتر
همراه با معرفی بخش دانشجویی خانه ریاضیات اصفهان
سخنران: علیرضا حقشناس
یکشنبه 17 اسفندماه، ساعت 14 الی 16
تخمین همزمان و شگفتیهای ابعاد بالا
دكتر كسری علیشاهی، عضو هئیت علمی دانشگاه صنعتی شریف
همراه با معرفی خانه ریاضیات اصفهان با حضور آقای دكتر علی رجالی
چهارشنبه 20 اسفندماه 1393 ساعت 14 الی 16
دانشگاه صنعتی اصفهان دانشكده علوم ریاضی سالن خوارزمی
کارگاه تفکر سیستمی
استفاده از بازی برای درک ساختارهای موثر در تخریب محیط زیست
مهندس محمد علی اسماعیلزاده
چهارشنبه 12 شهریور 93
ساعت 19- 15
خلاصه کارگاه :
هزاران سال است که موجودات از نعمت هایی که خداوند در کره ی زمین در اختیارشان قرار داده است استفاده میکنند. در طی دویست سال اخیر پیشرفت تکنولوژی قدرت بسیار زیادی به انسان ها داده است. استفاده از این قدرت اما در راستای حفظ محیط زیست و نعمت های خدادادی نبوده است. به همین دلیل طی این دویست سال انسان آسیب های بسیاری به محیط زیست زده است. خلیج های ماهیگیری بسیاری ظرفیت رشد ماهی های خود را از دست داده اند، جنگل ها به شدت تخریب شده اند، حیوانات بسیاری منقرض شده اند، لایه ازن که سپر دفاعی موجودات در مقابل اشعات مضر است آسیب دیده است، و آلودگی خاک، آب، و هوا سرنوشت تمام موجودات را به خطر انداخته است. در این میان اما مساله ی اصلی رشد تکنولوژی نیست، بلکه رویکرد انسان ها به استفاده از تکنولوژی است. انسان ها با استفاده از دانش و تکنولوژی می توانند زندگی سالمی که دوستدار محیط زیست باشد و توسعه ی پایدار را به وجود آورد رقم بزنند. همچنین با استفاده از دانش و تکنولوژی می توانیم آلودگی های گذشته را از بین ببریم و کره ی زمین را مکان مناسب تری برای زندگی موجودات کنیم.
در کارگاه های آموزش محیط زیست به کمک تفکر سیستمی، بازیهایی طراحی شده که با اجرای آنها دانش آموزان میتوانند درک بهتری از اهمیت محیط زیست و رابطه ی انسان با تکنولوژی و محیط زیست داشته باشند. همچنین دانش آموزان میتوانند نقش ساختارهای تصمیم گیری جمعی در بروز تصمیمهایی که منجر به تخریب محیط زیست می شوند را درک کنند. در این کارگاه برخی از این بازیها به معلمین معرفی میشوند و به صورت عملی اجرا میشوند.
درباره گروه آسمان
کارگاه تفکر سیستمی
آشنایی با مدلهای ذهنی و نقش آن در تصمیم گیری و یادگیری جمعی
مهندس محمد علی اسماعیلزاده
چهارشنبه 12 شهریور 93
ساعت 12:30 – 8:30
خلاصه کارگاه :
مدلهای ذهنی در واقع تصویری در ذهن ما در مورد این هستند که جهان چیست و چگونه تغییر میکند.
مدلهای ذهنی همچنین به ما میگویند که پدیدهها را در چه بازهی زمانی باید بررسی کنیم و چه محدودهای از عوامل را برای بررسی یک مساله باید در نظر بگیریم.
ما برای تصمیم گیری از اطلاعاتی که از دنیای اطرافمان دریافت میکنیم استفاده میکنیم.
اما تنها بخشی از اطلاعات در دسترس ما هستند و عوامل بسیار دیگری نیز باعث میشوند که ما همین بخش از اطلاعات را هم به درستی دریافت نکنیم.
مدلهای ذهنی ما نقش مهمی در دریافت، پردازش اطلاعات و تصمیم گیری بر مبنای اطلاعات دارند.
مدلهای ذهنی غلط میتوانند ادراک ما از دنیا و یادگیری ما از تجربیات خودمان و دیگران را تحت تاثیر قرار دهند.
در این کارگاه نقش مدلهای ذهنی در فرآیند تصمیم گیری و یادگیری جمعی را بررسی میکنیم و ابزارهای تفکر سیستمی برای بهبود مدلهای ذهنی و بهبود فرآیند تصمیم گیری و یادگیری جمعی را معرفی میکنیم.
درباره گروه آسمان

سخنرانی باعنوان جدول عمر
پروفسور Terry Mills
دوشنبه 10 شهریور 1393، ساعت 17:30
Life Tables
Terry Mills (Australia)I
Honorary Statistician at Bendigo Health
Emeritus Professor at La Trobe University
چکیده : جداول عمر، جداول ریاضی هستند که نرخ مرگ و میر را در سنین مختلف یک جامعه توصیف میکنند. بنابراین، جدول عمر شامل برخی ویژگیهای اساسی سلامت یک ملت است. در واقع میتوان امید به زندگی یک جمعیت را از جدول عمر محاسبه نمود. ما جداول عمر از نقطه نظر ریاضی بررسی خواهیم نمود.
علم احتمال اغلب به عنوان شاخهای دشوار از ریاضیات در نظر گرفته میشود. در حقیقت، جداول عمر روش مؤثر در معرفی مفاهیم احتمال را فراهم میکند. مفاهیمی دشوار از قبیل احتمال شرطی، زمانی که در چارچوب یک جدول عمر معرفی شوند، به آسانی درک خواهند شد. علاوه بر این، مدلهای ریاضی که اساس جداول عمر را تشکیل میدهند، ریاضی و محاسبات کاربردی و مفاهیم پیشرفتهتری در احتمال است. چند کتاب که حاوی اطلاعات در مورد جداول عمر است، در زیر بعنوان منابع ذکر شدهاند.
References
C.L. Chiang, Introduction to stochastic processes in biostatistics. New York: John Wiley, 1968.I
C.L. Chiang, Life table and its applications. Malabar, FL: Robert E. Krieger, 1984.Id
N. Keyfitz, Applied mathematical demography. New York: Springer-Verlag, 1977.I
N. Keyfitz and J. A. Beekman, Demography through problems. New York: Springer-Verlag, 1984.I
K. Namboodiri and C. M. Suchindran, Life table techniques and their applications. Orlando: Academic Press, 1987.I
J.H. Pollard, Mathematical models for the growth of human populations. Cambridge: Cambridge University Press, 1973.I
تری میلز در دانشگاههای سیدنی، ملبورن، فلوریدا و لاتروب تحصیل کرده است. در طول دوران کاری با تعدادی از بخشهای مختلف ریاضیات همچون نظریه تخمین، معادلات دیفرانسیل، آنالیز عددی، احتمال، تاریخ ریاضیات، نظریه گراف و آمار سروکار داشته است. برای وی، «آمار» بخشی از «ریاضیات» میباشد. زمانی که وی کارش را به عنوان یک ریاضیدان شروع نمود، تمرکز او بر روی ریاضیات محض بود. سالهای زیادی را به تدریس در دانشگاهها گذراند. اخیرا درگیر کاربرد ریاضیات در شاخه مراقبت سلامت و به عنوان یک ریاضیدان در بیمارستانی مشغول به کار است. وی اظهار میدارد که در آنجا فرصتهای زیادی برای ریاضیات کاربردی در حوزه سلامت وجود دارد. وی میگوید : گرچه من اکثر وقت خودم را به ریاضیات کاربردی اختصاص میدهم، ولی به یادگیری خود در ریاضیات محض نیاز دارم. من به تعاریف نیاز دارم، من نیاز دارم تا الگوریتمها را متوجه بشوم. نیاز دارم تا قادر به نوشتن برنامههای کامپیوتری به روشی منطقی باشم. یادگیریهای شما در ریاضیات میتوانند به طرق مختلف مورد استفاده قرار گیرند. این سخنرانی پیرامون جداول عمر است. جداول عمر خواص ریاضی گونه زیادی داشته و در حوزه سلامت کاربرد دارد. در این سخنرانی بر روی استفاده آنها در یادگیری احتمال تاکید خواهم داشت.
این یک جدول عمر پایه است. این جدول بر اساس دادههای مرتبط با مردان استرالیا بدست آمده است. در این جدول سن را در گروههای 10 ساله سنی داریم. در عمل گروههای 1 ساله سنی را را استفاده مینماییم، اما گروههای 10 ساله سنی برای مشاهده آسانتر است. تصور کنید که 100000 کودک تازه متولد داریم. این عدد دلخواه منشاء یا پایه جدول عمر نامیده میشود.
Age | l(X) | d(x) |
0 | 100,000 | 678 |
10 | 99,322 | 314 |
20 | 99,008 | 814 |
30 | 98,194 | 1,098 |
40 | 97,096 | 1,955 |
50 | 95,141 | 4,216 |
60 | 90,925 | 10,187 |
70 | 80,738 | 22,968 |
80 | 57,770 | 37,241 |
90 | 20,529 | 18,880 |
100 | 1649 | 1649 |
x = age سن
l(x) = number alive at age x.تعداد افراد زنده در سن مشخض
d(x) = number who die between age x and x+10. تعداد افرادی که بین سن مشخص و مشخص x وx+10 مردهاند
این عددی دلخواه است، اغلب 100000 در نظر میگیریم.
678 کودک بین سن 0 تا 9 سال مردهاند.d(0) = 678
So l(10) = 100,000-678=99322. بنابراین 99322 نفر تا سن 10 سالگی زنده ماندهاند.
d(10)=314 die. در طول 10 سال آینده
پس 99008 نفر از 100000 نفر اولیه تا سن 20 سالگی زنده میمانند. و به همین صورت تا پایین جدول مینویسیم. در نهایت 1649 تا سن 100 سالگی میرسند و همگی قبل از سن 110 میمیرند.
احتمال موضوع سختی میباشد، اما جداول عمر احتمال را ساده مینمایند. چقدر احتمال دارد که مردی تا 40 سالگی عمر کند. 100000 مرد 0 ساله در این جمعیت بودند. 97096 تای آنها تا 40 سال عمر کردند. احتمال اینکه مردی به سن 40 برسد برابر است با 97,096/100,000 = 0.97096 این یک محاسبه آسان بود. شما میتوانید ببینید که چطور نگاه به یک جدول عمر احتمال را آسان میسازد. احتمال اینکه مردی قبل از سن 80 بمیرد چقدر است؟ ما با 100000 مرد در سن 0 شروع کردیم، 57770 تای آنها تا 80 سال زندگی کردهاند، احتمال مردن قبل از سن 80 برابر 1- (57,770/100,000) = 0.4223. من این استدلال را «استدلال 1-احتمال برد» مینامیم. این بطور رایج در احتمال استفاده میشود.
احتمال شرطی اغلب به عنوان قاعدهای دشوار در نظر گرفته شده است. گرچه جداول عمر این قاعده را برای فهمیدن آسان میسازند. احتمال اینکه فردی 80 سال عمر نماید، به شرط آنکه به سن 20 سالگی رسیده باشد، چقدر است؟ با 100000 مرد شروع میکنیم، 99088 تای آنها به سن 20 سالگی رسیدهاند، اختمال آنکه مردی که 20 سال دارد به سن 80 برسد برابر است 57,770/99,008 = 0.5835. با فضای نمونه ما از گروه 100000 تای 0 ساله به 57770 تای 20 ساله تغییر یافت.ایده اساسی در احتمال شرطی فضای نمونه کوچکتر است.
فرض کنید 5 مرد را در نظر میگیریم. چقدر احتمال وجود دارد که همه آنها تا 80 سالگی عمر نمایند، احتمال اینکه یکی از آنها تا سن 80 زنده بماند برابر است با57,777/100,000. احتمال اینکه همه آنها تا سن 80 زنده بمانند برابر است با5^(57,777/100,000) . این با در نظر گرفتن این است که مرگ و زندگی 5 مرد مستقل از یکدیگر هستند.
مسالهای پیچیدهتر را در نظر بگیرید، کوین و بروس برادر هستند. کوین 20 ساله است. بروس 30 ساله است. همسر بروس صاحب یک پسر شده است. احتمال اینکه کوین و بروس و پسر متولد شده زنده باشند، وقتی که پسر به 10 سالگی رسیده باشد؟
این شامل محاسبه 3 احتمال است :
احتمال اینکه کوین به 30 سالگی برسد به شرط اینکه میدانیم کوین به 20 سالگی رسیده است : 98,194/99,008
احتمال اینکه بروس به 40 سالگی برسد به شرط اینکه میدانیم بروس به 30 سالگی رسیده است : 97,096/98,194
احتمال اینکه کودک از زمان تولد به 10 سالگی برسد : 99,332/100,000
حالا فرض کنید که زندگیهای این مردم مستقل از یکدیگر هستند. سپس احتمال اینکه کوین و بروس زنده باشند، زمانی که کودک به 10 سالگی میرسد برابر است با :
(98,194/99,008)*(97,096/98,194)*(99,332/100,000) = 0.9741
آیا منطقی است که بپنداریم زندگی کوین، بروس و کودک مستقل از یکدیگر هستند؟ شاید برخی ویژگیها باشد که به صورت ارثی بین مردان در فامیل پخش شده باشد. چون بروس، همسرش و پسرش به هم زندگی میکنند، آنها هدف ریسکهای مشابهی برای مردن هستند. گرچه برای اهداف شهودی ما این احتمالات را نادیده خواهیم گرفت.احتمالات درون جدول عمر ممکن است در طول 10 سال تغییر نمایند. گرچه آنها زیاد تغییر پذیر نمیباشند. در اینجا مسالهای را در راستای به کارگیری ریاضیات مشاهده کردید. باید هر فرضیهای را در محاسبات درگیر نموده و ببینیم چگونه آنها در عمل مورد استفاده قرار میگیرند.
اکنون به یکی از مهمترین ویژگیهای جدول عمر میپردازیم- محاسبه امید به زندگی جمعیت.امید به زندگی به عنوان میانگین تعداد سالهای عمر مردم در جمعیت تعریف شده است. با حرف E مشخص شده است.
با 100000 نفر در سن 0 شروع کردیم. پس E برابر است با میانگین تعداد سالهای عمر شده که برابر است با مجموع سالهای عمر شده تقسیم بر 100000.
678 نفر بین سن 0 و 10 سال مردهاند. بیایید بپنداریم که بر اساس میانگین آنها در 5سالگی مردهاند. پس این 678 نفر مجموعا 5*678 سال عمر کردند. سپس 314 تا از مردم بین سن 10 و سن 20 مردند. بیایید بپنداریم که بر اساس میانگین آنها در 5سالگی مردهاند. بنابراین آنها قبل از اینکه مرده باشند 15 سال عمر کردند. پس این 314 نفر بطور مجموع 15*314 سال عمر کردند. سپس 814 نفر بین سن 20 و سن 30 مردند. بیایید بپنداریم که آنها بطور میانگین در سن 25 مردهاند، پس 25 سال قبل از مرگشان عمر نمودهاند. پس این 814 نفر مجموعا 25*814 سال عمر کردند. پس مجموع تعداد سالهایی که عمر کردهاند، برابر است با 5*678+15*314+25*814+… و بنابراین E برابر است با
E = (5*678 + 15*314 + 25*814 + … )/100,000 = 79.0
پس بطور میانگین مردان استرالیایی تا سن 79.03 سال عمر میکنند.
تصادفی بودن تقریبا با هرچیزی در هم آمیخته است. تعجبی نیست که احتمال نقشی مهم در ریاضیات مدرن و کاربردهای آن بازی میکند. در این سخنرانی توضیح داده شد که چگونه جداول عمر میتوانند مورد استفاده برای شرح قواعد پایه در احتمال قرار بگیرند. جداول عمر همچنین به ما فهم و برداشتی از مرگ و زندگی افراد یک جامعه میدهد. آنها در مطالعات سلامت بسیار مورد استفاده هستند. شما میتوانید جداول عمر را برای محاسبه امید به زندگی که کلید اندازه گیری سلامت و خوش زیستی جمعیت است به کار بگیرید. در کار من در آمار سرطان، جداول عمر نقشی مهم در محاسبه آماربقا بازی مینمایند.

نخستین بنیانگذاران ریاضیات در جهان
اکبر زمانی
چهارشنبه 15 مرداد 1393، ساعت 17:00
خلاصه سخنرانی :
در این سخنرانی ابتدا راجع به ریاضیات بابلی، مصری صحبت شده و سپس به طور مختصر کارهای فیثاغورسیان، اقلیدس، خوارزمی خیام، دکارت، نپر و نیوتون بررسی میگردد.
تاریخچه تکامل دستگاههای اعداد
پیام سراجی
چهارشنبه 15 مرداد 1393، ساعت 18:15
در این سخنرانی، به طور خلاصه، به تاریخ تکامل دستگاههای اعداد طبیعی و حقیقی، نظریه مجموعههای نامتناهی و همچنین نکاتی تاریخی در مورد بعضی اعداد خاص، مانند عدد نپر و عدد پی میپردازیم.
دیدگاه بیزی بر خوشهبندی دادهها
وحید پرتوی نیا، دانشکده پلیتکنیک مونترال، کانادا
شنبه 18 مرداد 1393، ساعت 17:30
با خوشوقتی فراوان به اطلاع تمام همکاران دانشگاهی، دانشجویان، دبیران محترم کارشناسان و دانشآموزان علاقهمند میرساند که سمیناری با موضوع دیدگاه بیزی بر خوشهبندی دادهها، توسط آقای دکتر وحید پرتوینیا از دانشگاه پلیتکنیک مونترال، در روز شنبه 18 مرداد 1393، ساعت 17:30 در محل خانه ریاضیات اصفهان برگزار خواهد شد. شرکت برای عموم آزاد است.
چکیده : خوشه واژهای است که اکثر ما ایرانیان با آن آشنایی داریم، از خوشه گندم، انگور و خرما گرفته، تا یارانه نقدی. منظور ما از خوشهبندی، در این سخنرانی، نحوه گروهبندی دادهها است. خوشهبندی، اولین مرحله استخراج دانش و اطلاعات از دادهها است و بنابراین یکی از مهمترین مسائل در هر زمینه علمی-تحقیقاتی به شمار میرود. در این سمینار علل چالش برانگیز بودن مسئله خوشهبندی و اینکه چگونه بعنوان یک مسئله ریاضی تعریف میشود، بررسی خواهد شد.
آماردانان، جهان پیرامونشان را بر اساس مدلهای احتمالاتی درک و تحلیل میکنند و در این سخنرانی چنین دیدگاهی را برای خوشهبندی دادهها معرفی میکنیم. توماس بیز، توسط قضیهای مهم در آمار، روشی برای ترکیب وضعیتهای عدم قطعیت و اطلاعات پیشین را با اطلاعات جمعآوری شده از دادهها مطرح میکند، که ما در انتهای سخنرانی، کاربرد روش بیز را در نظریه خوشه بندی مورد نقد و بررسی قرار میدهیم.


برنامه سخنرانیهای عمومی خانه ریاضیات اصفهان
دوشنبه 25 فروردین 1393 ساعت 17 – 16 | History and Philosophy of Mathematics for Teacher’s Education | University of Siegen | Prof. Gregor Nickel |
سه شنبه 26 فروردین 93 ساعت 17:30 | Proof – Aspects of a strange phenomenon between freedom and enforcement | University of Siegen | Prof. Gregor Nickel |
شنبه 30 فروردین 93 ساعت 17 | Flipping the classroom | University Utrecht, Holland | Roeland Hiele |
شنبه 30 فروردین 93 ساعت :55 17 | A mathematical analysis of the dome of the shrine of Shah Nematollah Vali at Mahan | Research Group in History of Mathematics | Vincent Karels M.Sc |
شنبه 30 فروردین 93 ساعت 18:15 | Abu Rayhan Biruni in the 15th/21th centuryفایل کامل سخنرانی | Professor Jan P.Hogendijk |
History and Philosophy of Mathematics for Teacher’s Education
The talk will analyse various functions of history and philosophy of mathematics as a tool to improve the quality of teacher’s studies. In the second part these two disciplines will be discussed as a goal in themselves – being an essential part of any mathematical literacy. In a third part I will briefly report some of my concrete experiences from an integration of history and philosophy to teachers’s studies at Siegen University.
Proof – Aspects of a strange phenomenon between freedom and enforcement
Proofs play a major role in the everyday life of any mathematician. Undoubtedly, since the time of the ancient Greeks mathematics deals to a large extent with `proofs’. However, the question for the functioning and the function of mathematical proofs remains open. Working mathematicians agree, that a proof proves, but do not ask, how this really works. The talk will discuss various `non-formal’ aspects of mathematical proof – mostly regarding a proof as a special type of communication. Thereby we also refer to the classical controversy in the philosophy of mathematics which tried to decide whether proof is either synthetic or analytic.
Flipping the classroom
Using specific examples I will show how instruction videos can be used to expand the possibilities in and bring variety and interactivity to classroom teaching. This approach can be called the flipping-the-classroom model. Together with the audience, we will reflect on the following questions: what are the strengths, weaknesses, opportunities and threats of this flipping-the-classroom model? What are the possibilities in class?
A mathematical analysis of the dome of the shrine of Shah Nematollah Vali at Mahan
Using modern computer methods and photos of the entire dome in Mahan, we have analyzed the pattern on the dome and its possible design. According to our analyses, which we will present during the talk, the number 11 had a significant influence at various stages of the design. We will show several approaches but have not yet been able to explain all details in the interesting design.
Abu Rayhan Biruni in the 15th/21th century
Abu Rayhan Biruni (born 365 H.Q. /973 CE, died ca. 440 H.Q. / 1048 CE), was one of the most important astronomers and mathematicians of the medieval Islamic tradition. He also wrote extensively on chronology, history and Indian culture and astronomy and has received universal praise for his objective approach and his respect for different religions and cultures. The talk will give an overview of Biruni’s extant (and lost) work, listing the number of extant manuscripts, and the published editions and translations into many languages. I will then indicate several (small and large) research projects on him that
can be done, and also some new questions that can be asked about him, using the new technology of the internet age (the 15th/21th century). In connection with this lecture, a special bibliographic website has been created http://www.albiruni.nl.

مقدمه شناخت شیوههای رشد پایدار کودکان “باز تعریف” جانبدارانه کودکی، بازی، آموزش و ریاضیات
** فایل سخنرانی **
سخنران : طغیان انگشتری
مکان : خانه ریاضیات اصفهان
زمان : 25 فروردین 1393، ساعت 17:30
چکیده :
تعریف هر مفهوم باید علاوه بر “جامع و مانع” بودن، توانایی بسط شناختی آن مفهوم را نیز برای ما مهیا نماید. سعی شده “کودکی” با توسل به کشفیات اخیر در مورد رشد مغز چنان “باز تعریف” گردد که در نهایت راهکاری برای دستیابی به شرایط رشد پایدار کودکان را در اختیار ما قرار دهد. در این شرایط ناچاریم به بازی کودکان، آموزش و همچنین چرایی نقش ریاضیات در رشد کودکان توجه ویژه نماییم.
Self similarity for Penrose and Isfahan pattern
Professor Jost –Hinrich Eschenburg
دانشگاه Augsburg آلمان
پنجشنبه 22 اسفند 1392، ساعت 17:00
چکیده : الگوهای مسطح میتوانند ایده بینهایت به دو روش مختلف بیان کنند : با تکرار (دوره تناوب) و یا توسط خود متشابهی، که در آن جزئیات مشابه در مقیاسهای مختلف ظاهر میشوند. طرحهای خود متشابهی کمتر از دوره تناوب آشکار است و در نتیجه این نوع طرح اغلب در هنر زیاد رخ نمیدهد…. یکی از سایتهایی طرح در آن رخ داده است، در شهر اصفهان روی درب امام و در یکی از ایوانهای مسجد جمعه و برخی از مکانهای دیگر. الگوهای این طرح 300 ساله بسیار شبیه به الگوهای aperidic است که توسط ریاضیدان Roger Penrose در حدود 40 سال پیش کشف شد. در واقع اتفاق تصادفی قابل توجه بین دو الگو وجود دارد. هر دو در ایده خود متشابهی و تقارن مکانی پنج وجهی مشترکند. با این حال، تفاوت وجود دارد : الگوی بکار رفته در طرحهای بناها در شهر اصفهان تقارن 10 وجهی داشته که با الگوهای پنروز شباهتی ندارند. با این حال، هر دو طرح الگوهای پنروز را نیز به ذهن میآورد. این طرحها یک الگوی جدیدی از پنروز را آشکار میکند که در آن تقارن تقریبا 10 وجهی مخفی است. این الگوی جدید از طرحهای تصویری که از تصویر شدن قسمتی از شبکه تناوبی 5 وجهی در صفحه بوجود میآیند، تبعیت نمیکند. بنابراین کار هنری ایرانی 300 ساله تاثیراتی در ریاضیات امروزه داشته است.


آموزش مجازی
پروفسور پیتر بوون، دانشگاه اوتریخ هلند
دوشنبه 12 اسفند 1392، ساعت 17
Clockwork gearing in ancient Greece and Medieval Islam
خانه ریاضیات اصفهان
شنبه 10 اسفند 1392، ساعت 17:00
پروفسور J.L.Berggren از دانشگاه Simon Fraser University, Canada، روز شنبه 10 اسفند 1392 از ساعت 5 بعدازظهر
خلاصه سخنرانی :
با کشف تصادفی یک کشتی غرق شده باستان در سال 1900 در جزیرهای در کشور یونان به نام Antikythera، قطعات پوسیده شده جسمی که معلوم شد یکی از قدیمیترین نمونه شناخته شده از چرخ دندههای دقیق است، مرمت شد. مطالب در نظر گرفته شده در این سخنرانی، داستان شگفت انگیزی است از چگونگی تلاشهای مشترک باستان شناسان، مورخان علم و آخرین تکنولوژی تصویربرداری، که به بازسازی کامپیوتر چرخدندهای باستانی یونان بهمراه بازنگری کلی از دیدگاه ما در رابطه با فنآوریهای یونانی، منجر شد. در این مکانیسم، تاریخ جامعی از چرخدندههای بجا مانده از قرون وسطی اسلامی، از جمله اسطرلابهای بیرونی و محمد بن ابی بکر که شامل بسیاری از ویژگیهای مشابه در مکانیسم Antikythera است، دنبال خواهد شد.
Dr. Len Berggren is Emeritus Professor of Mathematics at Simon Fraser University in British Columbia, Canada, He was introduced to the Antikythera mechanism by Prof. Derek Price, who did the first study of that instrument using imaging technology, during a visiting year at Yale University in 1972. Prof. Berggren has lectured at major universities around the world and is known internationally as an authority on the history of mathematics and astronomy in ancient Greece and medieval Islam. Among his publications are translations of Greek scientific works by Euclid, Claudius Ptolemy and Geminus, as well as Episodes in the Mathematics of Medieval Islam, which has been translated into German and Farsi.d
Decoding the Heavens: A 2000-Year old Computer and the Century-long Search to Discover Its Secret
کاربرد ماشین حساب در آموزش ریاضی
دوشنبه 21 بهمن 1392، ساعت 17
Murdoch University, Australia
روز دوشنبه 21 بهمن 1392 از ساعت 5 بعدازظهر
خلاصه سخنرانی :
در این سخنرانی كه ترجمه آن را همراه دارد بیشتر مخاطبین، آموزگاران دبستانها هستند و نحوه استفاده از ماشین حساب توسط كودكان ارائه میشود.
در ادامه آقای Miyakawa از شرکت کاسیو در رابطه با روند پیشرفت تکنولوژی در آموزش و آقای دکتر داوودی در رابطه با استفاده از ماشین حساب در آموزش ریاضی سخنرانی خواهند داشت. در پایان نیز مسابقهای با طراحی دایا سیستم برگزار خواهد شد و به برندگان جوایزی اهداء میشود.
نگاهی به تاریخ ریاضیات در ایران دوره قاجار

آقای دکتر فرید قاسملو، عضو گروه تاریخ علم بنیاد دائره المعارف اسلامی
پنجشنبه 10 بهمن 1392، ساعت 17:30، خانه ریاضیات اصفهان
چکیده : به نظر میرسد معاصر بودن یا به تعبیر دیگری معاصر شدن تاریخ ایران، در جایی از حکومت قاجارها در ایران (دوران 1210 تا 1344) قرار میگیرد. از نظر علمی و از نظر بررسی درباره منابع جستجو در تاریخ ریاضیات معاصر ایران، نیز باید گفت که تمامی مؤلفههای اجتماعی تعریف تاریخ معاصر ایران (از جمله شامل رواج روزنامهها، ورود صنعت چاپ و …) که هرکدام جایی در بررسی تاریخ ریاضیات معاصر ایران دارند، نیز در دوران قاجار نیز در دوران قاجار پدید آمدهاند. بر همین اساس این دوران یکی از مهمترین دورانهای تاریخ ایران و نیز یکی از مهمترین دورهها برای بررسی علم در ایران به شمار میآید.
در دوران قاجار دستکم با سه واقعه تاریخی سروکار داریم، افتتاح دارالفنون (1268ق)، واقعه رژی(130ق) و انقلاب مشروطیـت ایران (1323ق). اما همانگونه که خواهیم دید …
نگاهی به وضعیت ریاضیات و علوم دقیق در تاریخ اجتماعی ایران
آقای دکتر رضا مرادی غیاثآبادی
نویسنده و پژوهشگر در حوزه تاریخ
پنجشنبه 21 آذر1392، ساعت 16:30
در این سخنرانی به موضوعات زیر پرداخته میشود :
- نقاط اوج و حضیض دانش ریاضیات در کدام دورههای تاریخی ایران بوده است و چرا؟
- توجه یا بیتوجهی عمومی به دانش ریاضیات در کدام دورههای تاریخی ایران بوده است و چرا؟
- نگاه عمومی جامعه به ریاضی و علوم دقیق و نیز دانشمندان آن چگونه بوده است؟
- سرنوشت عمومی ریاضیدانان در جامعه ایرانی چگونه بوده است؟
- آیا دستاوردهای ریاضیات ایرانیان به اندازهای که در دنیا شهرت دارد، در ایران نیز شناخته شده هستند؟
- وضعیت ریاضیات، پژوهشهای ریاضی و نیز منابع مکتوب ریاضیات در ایران امروز چگونه است؟
دوره آشنایی مقدماتی با نظریه نسبیت عام اینشتین
مدرس: فرهنگ لران (استاد دانشگاه صنعتی اصفهان)
شروع دوره: چهارشنبه 10 مهر 92 ساعت 16:30
پایان مهلت ثبتنام: دوشنبه 8 مهر 1392
بیش از یک صد سال از ظهور نظریههای نسبیت خاص و عام اینشتین میگذرد. به برکت این نظریهها، جهان هستی در نظر انسان، از جهانی ساکن و ایستا به جهانی در حال انبساط بدل گشته که نقطه آغازی در حدود سیزده میلیارد و هشتصد میلیون سال پیش دارد. مخابرات ماهوارهای و سامانههای مختصهیابی نمونههایی از تاثیر این دو نظریه در دستیابی به فنآوریهای نویناند.
خانه ریاضیات اصفهان در راستای اهداف خود در ترویج علم، دوره «آشنایی مقدماتی با نظریهی نسبیت عام اینشتین» را برگزار میکند. این دوره شامل شش جلسه است که در شش هفته متوالی تشکیل میشوند. هر جلسه یک ساعت و نیم به علاوه ده دقیقه استراحت و ده دقیقه پرسش و پاسخ خواهد بود. موضوع جلسات به ترتیب از این قرار است :
- مفهوم ناظر و دستگاه لخت، فضا و زمان کلاسیک و نسبیت گالیله.
- نسبیت خاص و مساله انقباض طول و اتساع زمان، مفهوم فضازمان به جای فضا و زمان.
- قانون سوم نیوتن و تعریف لختی، اصل ماخ و ساختار موضعی فضا زمان.
- تعریف انتقال موازی در فضا زمان ناتخت، تعریف خمش فضا زمان و ارائه معادله اینشتین.
- تحلیل فضا زمان فریدمن-روبرتسون-واکر، انفجار بزرگ و مساله ثابت کیهانشناختی.
- تحلیل حل شوارتزشیلد، ساختار سیاهچاله و مساله اطلاعات.
برنامهریزی درسی ریاضی
سخنران : آقای دکتر مهدی رجبعلی پور، استاد دانشگاههای کرمان و تورنتو کانادا
دوشنبه 23 اردیبهشت 1392، ساعت 17:30
The qanat as the mother of aqueducts
سخنران : Wilke Schram M.Sc
سه شنبه 17 اردیبهشت 1392، ساعت 18:30
چالشهای آموزش ریاضی مدرسهای در ایران
آقای دکتر علی رجالی، دانشیار دانشگاه صنعتی اصفهان
دوشنبه 25 دی 1391
چالشهای آموزش ریاضی مدرسهای در ایران
جناب آقای دکتر سعید گازر
استاد دانشکدههای برق و کامپیوتر- ریاضی و آمار
خلاصه سخنرانی:
In this talk, we intuitively use the human cognitive system in order to give ideas and a roadmap for future technologies in a lay language. The goal of cognitive distributed statistical signal processing technologies is to monitor events and changes in distributed infrastructures such as wireless communications, power grids and radars. Traditional network infrastructure incorporates little to no cognition. Cognition-based systems can intelligently and dynamically alter and reconfigure themselves to enhance resource management. They can also learn from past situations, decisions and actions in order to improve future outcomes. Advanced and low-cost algorithms are the key to next-generation technology. These infrastructures hold a significant place in the economy in terms of employment and revenue. The cognitive management of scarce distributed resources promises to enhance the efficiency of these critical infrastructures. As modern society increasingly relies on mobile connectivity, spectrum demand is increasing. This ever-increasing demand has led to re-evaluation of spectrum utilization and highlighted the necessity for cognitive technologies to gather and act on information about the medium and users to improve network efficiency, save energy, and lower costs. Many problems to be solved
arise when distributed elements must make a collective set of decisions and have limited ability to exchange information
ریاضی خانههای ریاضیات
دکتر امید علی کرم زاده
استاد دانشگاه شهید چمران اهواز
روز شنبه 6/8/1391 از ساعت 4:30 بعدازظهر
ریاضی خانههای ریاضیات – اتصال ماری
(ویرایش به زبان انگلیسی English Version )
ویکتور بلاسجو و ویلفرد دی گراف
روز شنبه 6 اسفند 1390 از ساعت 3 بعدازظهر
کاشانی اولین ریاضیدانی است که عدد پی را تا 16 رقم اعشار تعیین کرده است. این کارگاه به مقایسه روش کاشانی برای تعیین عدد پی با روش دیگری که در همان زمان در مکتب مدهاوا در هند کشف شده است، و همچنین پیشرفتهای مرتبط در قرن 17 میلادی توسط ویلیبرورد اسنلیوس در هلند میپردازد. بوسیله محاسبات دستی، شرکت کنندگان در کارگاه کارایی قابل توجه روش کاشانی را آزمایش خواهند کرد.
دو ابزار از غیاثالدین جمشید کاشانی برای محاسبه نجومی
پروفسور پیتر هوخندایک استاد دانشگاه اترخت هلند
روز شنبه 6 اسفند 1390
جمشید كاشانی در “نزهت الحدایق” ساختار و طرز كار دو ابزار را شرح داده است كه برای تعیین موقعیتهای
نجومی بدون محاسبه ایجاد كرده بود. این ابزارها عبارتند از طبق المناطق، برای تعیین موقعیت نجومی (شامل عرض
جغرافیایی)، و لوحالاتصالات برای تعیین ساعت دقیق اتصالات (اقترانات نجومی). نزهت الحدایق در سال 819) 1416
میلادی) نوشته شده و در سال 829) 1426 میلادی) تجدیدنظر شده است، و در حدود سال 900) 1500 میلادی)
ابزارهایی مشابه در نوشتهای فارسی توصیف شدهاند كه توسط ای. اس. كندی در 1960 میلادی منتشر شده است. در این
سخنرانی این ابزارها و بازسازی مجدد آنها توسط پرفسور فوات سزگین (از موسسه تاریخ علوم اسلامی- عربی در
فرانكفورت و موزه تاریخ علم و تكنولوژی در اسلام در استانبول) معرفی خواهند شد. سپس به بحث پیرامون برخی
مسایل تاریخی مرتبط با وضعیت این ابزارها در تاریخ علم تمدن اسلامی خواهیم پرداخت.
شنبه 6 اسفند 1390
پروفسور Benno Van Dalen، استاد دانشگاه اترخت هلند
روز شنبه 6 اسفند از ساعت 5 بعدازظهر
“غیاث الدین جمشید کاشانی به خاطر محاسبات فوقالعاده دقیقش از سینوس 1 درجه و عدد پی مشهور است، این محاسبات در اروپا تا تقریبا دو قرن پس از او بهبود نیافتند. این سخنرانی مروری است بر واقعیاتی که پیرامون زندگی کاشانی و دستاوردهای علمی مهم او میدانیم. به ویژه نگاهی میاندازیم به :
- نامههایی که کاشانی به پدرش در مورد فعالیتهای علمی انجام شده در رصدخانه بنا شده در سمرقند توسط پادشاه تیموری، الغ بیگ نوشته است،
- کتاب جامع نجوم او با جداولی با عنوان زیج خاقانی و روشهای نوآورانهای که در آن کتاب یافت میشود :
- روش محاسبه او از سینوس 1 درجه و عدد با دقت 17 رقم اعشار،
- و سر انجام تاثیر او بر زیج الغ بیگ و جدول فوق العاده دقیق او از سینوس.”
اثبات قضیه آخر فرما
علی رجالی
29 دی 1390
خلاصه سخنرانی:
قضیه آخر فرما به عنوان یک سوال مقدماتی که 350 سال ریاضیدانان را به خود مشغول داشته بود و
رکورددار بیشترین حل غلط ارائه شده بود حائز اهمیت نیست، بلکه چنانچه توضیح خواهیم داد تلاشهای
نافرجام برای اثبات آن سبب ایجاد شاخههای مهمی چون جبر جابجایی و هندسه جبری حسابی گردید و شگفتا
که حل نهایی آن همافقهای جدیدی در نظریه اعداد، هندسه جبری، نظریه نمایش و بسیاری شاخههای دیگر
برای ما گشوده است.
آقای یونس کرامتی
از پژوهشکده میراث مکتوب
خلاصه سخنرانی:
1 .بنیانگذاری جبر و تعریف موجودات جبری توسط خوارزمی به قیاسدستگاه شمار دهگانی
2 .دسته بندی و حل معادلات درجۀ دوم، سوم و بالاتر
3 .حل عددی معادلات درجۀ سوم و بالاتر
4 .نمونههای جالبی از آلگوریتم حل مسائل در آثار کاشانی
5 .نکاتی دربارة روش خطأین و اشارة جالب کاشانی به شرایط امکان استفاده از این روش
آثار ازدست رفته ابوسهل کوهی (ریاضیدان)
Professor Len Berggren
استاد دانشگاه کانادا
روز شنبه 7 اسفند 1389 از ساعت 5:30 بعدازظهر


علم، ترویج علم، و ترویج تفکر علمی
آقای دکتر منصوری استاد دانشگاه صنعتی شریف روز پنجشنبه 10 اردیبهشت 1388 از ساعت 5:30 لغایت 6:30 بعدازظهر
در محل سالن ادب، واقع در بلوار هشت بهشت، روبروی سازمان آموزش و پرورش اصفهان، کوچه شهید عقیلی، آمفی تئاتر ادب ایراد خواهند نمود. خلاصه سخنرانی: ما مسلمانان، نه تنها ایرانیان، به دلیل تاریخ پرافتخار علمیمان هنوز، پس از 200 سال که از آشنایی ما با غرب میگذرد، با مفهوم علم نوین مشکل داریم: علم سنتی محصور در علوم دینی را با علم به مفهوم نوین آن یکی میگیریم. توسعه و حضور در صحنه جهانی برای ما ممکن نیست، مگر اینکه با این مفهوم نوین کنار بیاییم: ابتدا آن را درک کنیم، سپس تکلیف خود را با آن روشن کنیم. برای رسیدن به این مرحله و گذار از آن چارهای نیست جز ترویج تفکر علمی، که با ترویج علم به مفهوم ترویج دانستههای علمی متفاوت است.
Issues in Contemporary Mathematics Education in France
Professeur a l’Universitede Versailles Saint-Quentin, France
روز دوشنبه11 آذر 1387 ساعت 5:00 بعدازظهر
در محل خانه ریاضیات اصفهان برگزار شد. در این سخنرانی که با حضور جمعی از اساتید و معلمان ریاضی و دانشجویان علاقمند برگزار شد، آقای پروفسور اندلر درباره نظام آموزشی دوره های راهنمایی و متوسطه در فرانسه صحبت نمودند.

در ادامه برنامههای سخنرانیهای عمومی خانه ریاضیات اصفهان، با خوشوقتی فراوان به اطلاع تمام همکاران دانشگاهی، دانشجویان، دبیران محترم ریاضی و آمار، کارشناسان و دانشآموزان علاقهمند میرساند که :
پیام سراجی روز پنجشنبه1 اسفند 1387 ساعت 17:00
یک سخنرانی تحت عنوان :
مروری بر چالشهای مبانی ریاضیات
در محل خانه ریاضیات اصفهان ایراد خواهند نمود. خلاصه سخنرانی: در این سمینار ابتدا مروری بر مهمترین مشکلات و چالشهایی که از دوره یونان باستان تا دوران معاصر در مبانی ریاضیات مطرح شدهاند خواهیم داشت و سپس به نقش این چالشها در ایجاد مکاتب مختلف در فلسفه ریاضی میپردازیم. برخی چالشها که مختصرا مرور خواهند شد عبارتند از: کشف اعداد گنگ، بینهایت کوچکها، پارادوکس راسل، اصل انتخاب و اصول کاردینالهای بزرگتر در نظریه مجموعهها.
Greek geometric art
سخنران آقای پروفسور Konstantinos Nikolantonakis
University of Western Macedonia – Greece
Department of Prima
در روز شنبه 30 آذر 1387 ساعت 5:00 بعدازظهر در محل خانه ریاضیات اصفهان ایراد خواهند نمود.


جلسه سخنرانی آقای پروفسور” Konstantinos Nikolantonakis” روز شنبه 30/9/87 در خانه ریاضیات اصفهان و با موضوع « Greek geometric art» برگزار شد.
در این سخنرانی آقای پروفسور Nikolantonakis در ابتدا به ارائه تاریخچهای از هنر و ارتباط آن با ریاضی در تاریخ یونان و آثار بهجا مانده از آن دوران پرداختند و با پرداختن به برخی اشیاء تاریخی یونان، درباره تأثیر هندسه غیر رسمی در ساخت این آثار صحبت کردند.در ادمه ایشان به نقش و تأثیر مطالعه و بررسی هندسه غیررسمی (informal geometric) در رشد و ارتقای آموزش ریاضی در مدارس ابتدایی، اشاره کردند و توضیحات تکمیلیتری را در اینباره ارائه نمودند. متن کامل این سمینار را در این لینک ببینید.
خلاصه سخنرانی :
In our paper we are going to present the Greek geometric art which has been developed in two phases: 1) from 1100 to 900 B.C. called proto-geometric style and 2) from 900-700 B.C. called geometric style. In each case we are going to present a series of ceramic vases of these periods and we are going to discuss the characteristics of this art. In the first part we will focus on the analysis of the appearance of geometric abstract figures, animals, humans and more complex representations of the protogeometric and geometric style. In the second part we are going to discuss ways for using this material for educational purposes in the context of teaching geometry in the first grades of Primary school (draw lines, draw figures with and without instruments, find patterns etc.
Teaching students to think mathematically
سخنرانی خانم Kaye Christine Stacey
از دانشگاه ملبورن
روز شنبه 19 مرداد 1387 از ساعت 18:00 در خانه ریاضیات اصفهان
و با حضور جمع زیادی از علاقمندان به ریاضی، و به ویژه آموزش ریاضی
خلاصه سخنرانی :
I will discuss a mathematical problem which can be used to teach students to thinkmathematically and to solve mathematical problems that are unfamiliar and new tothem. The processes of looking at special cases, generalising, conjecturing andconvincing will be highlighted through these examples, These are key processesin thinking mathematically.
مقالهای که در لینک زیر قابل دسترسی است، مقالهای است که، خانم Kaye Christian Stacey در دهمین کنفرانس آموزش ریاضی ایران (یزد)، ارائه نمودند . ایشان لطف نمودند و این مقاله را در اختیار ما قرار دادند تا برای استفاده عموم علاقمندان به ریاضی در دسترس باشد.
عنوان نخستین مقاله : “The transition from arithmetic to algebraic thinking”
عنوان دومین مقاله : “Students’ understanding of decimal notation – a longitudinal study of learning“
سمیناری پیرامون وضعیت ماشین حسابهای علمی و مهندسی
به اطلاع علاقهمندان میرساند که روز سه شنبه23 بهمن 1386 ساعت 17:30 سمیناری پیرامون وضعیت ماشین حسابهای علمی و مهندسی در دنیا توسط آقای Matsui (مدیر بخش خاور میانه ماشین حسابهای کاسیو در ژاپن) و سپس در ساعت 17:45 کارگاهی آموزشی پیرامون کارکردن با ماشین حسابهای مهندسی کاسیو در ریاضیات توسط آقای راجی در محل خانه ریاضیات اصفهان برگزار میگردد.
کارگاه یکروزه اسطرلاب ایرانی بعد از ظهر روز شنبه 8/10/86،از ساعت 13 الی 15و همزمان با عید سعید غدیر در خانه ریاضیات اصفهان وتوسط دو دانشجوی هلندی به اسامی Wifred de Granf , Eric van Lit از دانشگاه اترخت هلند برگزار شد.
این گارگاه بر اساس گارگاهی است که توسط آقای پروفسور یان هوخندایک به دفعات در کشور هلند و ایران برگزار شده است. در ابتدا کلیاتی درباره اسطرلاب و معرفی ویژگیهای آن گفته شد و سپس از شرکت کنندگان خواسته شد تا دو تمرین داده شده در کارگاه را حل کنند و با طریقه کار و استفاده از اسطرلاب آشنا شوند . اسطرلاب یکی از پرکاربردترین ابزارهای جهان اسلام و مغرب زمین بوده است،که بر اساس اصول ریاضی که مربوط به یونان باستان می باشد ساخته شده و در دوران اسلامی ، از حدود 200 هجری قمری به بعد ،بسیار مورد استفاده قرار گرفت.
اسطرلاب و یادگیری روش کار با آن برای شرکت کنندگان، که تعدادشان به بیش از 20 نفر می رسید، بسیار جذاب بود و باعث شد که با جدیت حل تمرین ها را دنبال کنند. برگزاری چنین گارگاهایی باعث می شود که اصول پیچیده ریاضی در قالبی قابل فهم و ساده برای همه ارائه شود و همین امر موجب جذابیت ریاضیات برای همه و عمومی شدن آن می گردد، که از اهداف اصلی خانه ریاضیات اصفهان می باشد.


در ادامه سخنرانیهای عمومی خانه ریاضیات اصفهان، روز پنجشنبه 24 آبان 1386 دکتر ابراهیم پور به ارائه سخنرانی تحت عنوان: فرکتال ها و کاربردهای آن در شناسائی تصاویر پرداختند.
خلاصه سخنرانی :
فرکتالها المانهایی ریاضیاند که ویژگیهای منحصربه فردی را از خود بروز میدهند. ویژگیهایی نظیر ابعاد کسری، تکرار و خود تشابهی و… .
چنین ویژگیهایی در برخی عناصر طبیعی نظیر برگ سرخس نیز مشاهده میشود. آنچه که این پدیده را دارای اهمیت میکند، بررسی این نکته است که چرا اشیا پیچیدهای نظیر برگ سرخس از قوانین ریاضی نسبتا سادهای که شکل آن را ایجاد میکنند تبعیت میکند؟ سوالات دیگری از این دست میتواند به شرح زیر باشد :
- ارتباط شکلهای فرکتالی با سیستمهای دینامیکی خاص، به ویژه سیستمهای آشوبی چیست؟
- بعد فرکتالی چیست و چگونه محاسبه میشود؟
- چگونه میتوان کدهای فرکتالی یک شکل را بدست آورد؟
- آیا میتوان از کدهای فرکتالی برای شناسایی تصاویر استفاده کرد؟
فیلم سمینار در کتابخانه خانه ریاضیات موجود است.
بیوگرافی مختصر ارائه کننده : دکتر حسین ابراهیم پور کومله دوره کارشناسی خود را دررشته مهندسی کامپیوتر(سخت افزار) با رتبه اول در دانشگاه صنعتی اصفهان در سال ۱۳۷۲ و دوره کارشناسی ارشد را در دانشگاه صنعتی امیرکبیردر گرایش هوش ماشین و رباتیک درسال ۱۳۷۵ به پایان رساند. سپس به عنوان عضو هیات علمی جذب دانشگاه کاشان شد و پس ازقبولی در امتحان دکتری بورس و اعزام، از سال ۱۳۷۹ عازم کشور استرالیا گشت. او پروژه دکتری خود را با عنوان “تکنیک های فرکتالی برای شناسایی چهره” در دانشگاه صنعتی کویینزلند با موفقیت به پایان رساند. دکتر ابراهیم پور پس از اتمام دوره فوق دکتری در دانشگاه نیوکاسل و همکاری با مرکز تحقیقات علمی استرالیا (csiro) به عنوان “Visiting Scientist” به ایران مراجعت و همکاری خود را با دانشگاه های کشور از سرگرفته است. از ایشان تا کنون حدود ۱۸مقاله در کنفرانس ها – مجلات و کتب معتبر علمی چاپ گشته است.
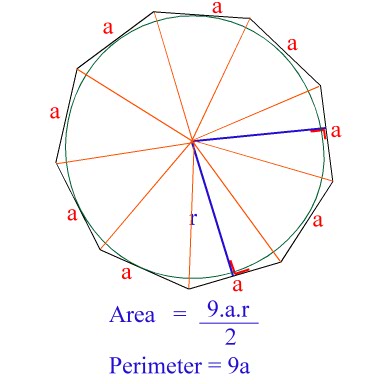
مقایسه روشهای ابوالوفای بوزجانی و ابوریحان بیرونی در تنظیم 9 ضلعی منتظم
سخنران دكتر چاووشی
در پنج عصر روز پنجشنبه 17 آبان 1386درمحل خانه ریاضیات اصفهان و با حضور 40 نفر از اساتید دانشگاه، معلمین ، دانشجویان و دانش آموزان برگزار شد. دكتر چاووشی با اشاره به شرح حال ابوالوفا از دیدگاه تاریخ ریاضی، از او به عنوان پیوند دهنده هندسه عملی با هندسه نظری یاد كرد، در این سخنرانی دكتر چاووشی با همكاری آقای زمانی نخست روش معماران را برای رسم 9 ضلعی منتظم مطرح كرده و سپس روشهای ابوالوفای بوزجانی و ابوریحان بیرونی را ارائه داده و نقاط ضعف وقوت هر یك از این روشها بازگو شد.
مقایسه روشهای ابوالوفای بوزجانی و ابوریحان بیرونی در تنظیم 9 ضلعی منتظم
در ادامه سخنرانیهای عمومی خانه ریاضیات روز پنجشنبه 17 آبان 1386 دکتر چاوشی به ارائه سخنرانی تحت عنوان “مقایسه روشهای ابوالوفای بوزجانی و ابوریحان بیرونی در تنظیم 9 ضلعی منتظم” پرداختند.
خلاصه سخنرانی :
9 ضلعی منتظم را نمیتوان به وسیله خطکش و پرگار ترسیم نمود. زیرا تعیین ضلع آن به یک معادله درجه سوم منجر میگردد. این شکل هندسی با اینحال مورد توجه معماران و هنرمندان اسلامی بوده و از آن برای نقوش تزئینی بهره بردهاند.
شاید به همین دلیل است که هم معماران و هم ریاضیدانان اسلامی روشهائی را برای رسم این شکل ارائه دادهاند.
در این سخنرانی، نخست روش معماران را برای رسم این شکل مطرح کرده و سپس روشهای ابوالوفای بوزجانی و ابوریحان بیرونی را ارائه داده، نقاط ضعف و قوت هریک از آنها را بازگو میکنیم.
فیلم سمینار در کتابخانه خانه ریاضیات موجود میباشد.
Psycho Acoustic
در ادامه سخنرانیهای عمومی خانه ریاضیات اصفهان شنبه 2/10/1385،آقای دکتر سعید گازر استاد دانشگاهQueen’s کانادا به ایراد سخنرانی با موضوع Psycho Acoustic پرداختند.
خلاصه سخنرانی :
در این سخنرانی ضمن اشاره به اصول شنوایی، ارتباط علوم ریاضی و روانشناسی را با آن بررسی و سپس به برخی از کاربردهای آن در زمینه کمک به ناشنوایان برای شنیدن اصوات و همچنین صنعت پرداخته میشود.
Teaching Mathematics as a Constructive and Creative Activity
روز پنجشنبه 15/6/1385 پروفسور جان میسن John Mason استاد دانشگاه Open لندن، با حضور در خانه ریاضیات اصفهان و آشنائی با فعالیتها وبرنامههای خانه، به ارائه سخنرانی تحت عنوان :
Teaching Mathematics as a Constructive and Creative Activity پرداختند.
خلاصه سخنرانی :
I will invite participants to engage in some mathematical tasks which call upon the learner to construct mathematical objects, and offer the conjecture that this not only engages learners actively, but calls on their natural powers to make sense of mathematics and to make sense mathematically. Using construction tasks in teaching not only displays mathematics as a constructive activity, but engages the teacher in onstructive and creative activity as well
فیلم سخنرانی ایشان در کتابخانه خانه ریاضیات موجود می باشد.
Mathematics as a constructive activity: learners generating examples
مروری بر مجموعههای تعیینکننده در ترکیبیات
دکتر محمودیان
دبیرستان بهشتآیین، 7 آبان 1380
ترکیبیات به دنبال الگوهایی است که در مجموعههای متناهی میتوانند وجود داشته باشند. مجموعههای تعیینکننده عبارتند از اینکه از یک الگو در ریاضیات چه مشخصاتی باید داده شود تا آن الگو به طور منحصر به فرد مشخص شود. مفهوم تطابق کامل در گرافها به مجموعههای تعیینکننده مربوط میشود و موضوع این سخنرانی نیز همین ارتباط است. در انتها نیز تعدادی از کاربردهای عملی مرتبط با موضوع مورد بررسی قرار گرفتهاند.
تأکید بر خردگرایی
پروفسور رضا
خانه ریاضیات اصفهان 20-22 آبان 1379
مصادف با تولد امام زمان (عج)
خانه ریاضی اصفهان به صورت کوچک مینماید. کتابخانه محدود، چند صد رایانه، یک عدهای جوان و عدهای رهبران و استادان معتقد و البته پیوند به اینترنت. اما در معنی بسیار بزرگ است. اینجا خانقاه دانشپژوهان خرد دوست است که میخواهند به دنیای دانش پیوند یابند. اینجا کاروانسرای سر راه جوانان خردجوست. معروف است که افلاطون هم چنین خانهای داشت و بر سر درب آن نوشته بود هرکه هندسه نمیداند به اینجا راه ندارد. هندسه زبان استدلال و منطق است.
دلیل افول ما از دوره 500 ساله شکوفایی دانشمندان اسلامی-ایرانی چه بوده است؟
حدود 550 سال پیش، در سال 1450 میلادی، اختراع بسیار بزرگی صورت گرفت، چاپ گوتنبرگ. پس از این اختراع، 2000 جلد از کتابهای بزرگان اسلامی که بیشتر ایرانی بودند از عربی به لاتین ترجمه شد و موجب پایهگذاری دوره تجدد در اروپا شد و ما در ایران از این اختراع بزرگ استفاده نکردیم. ماشین چاپ در سال 1600 به اصفهان آمده ولی بیش از 150 سال از چاپ کتاب در ایران نمیگذرد و در این دوران هم بیشتر کتابهای غیر علمی چاپ شدند کتاب نیوتن ترجمه نشد. آیین خردگرایی در غرب در بافت عمومی آن نفوذ کرد درحالی که در شرق چنین نبود و در متن فرهنگ ما جای نگرفت. بیخبری ما زیان دارد به همان اندازه که خودباختگی زیان دارد.
آینده علمی و صنعتی کشورها در خانههایی مانند خانه ریاضیات شکل میگیرد. در خانه ریاضی افراد زبان خرد را فرا میگیرند. آشنایی با این زبان تنها شرط ورود به کشور دانش است. اینترنت فرصتی که در 550 سال پیش، با اختراع چاپ گوتنبرگ در اختیار جهان غرب قرار گرفت، در اختیار کل جهان قرار داده است و این عقبافتادگی را قابل جبران کرده است. من مهمترین کلید بازگشت ایران به ردههای بالا و زندگانی شکوفا را گسترش حسابگری و واقعبینی یعنی خردگرایی میدانم و تأسیس خانه ریاضیات و کوشش انجمنهای ریاضیدانان در سال 2000 را دروازه سمبلیک بازگشت به دوران بزرگی و سروری میدانم.
هویت ملی قوم ایرانی تا به حال بیشتر بر پایه هنر بویژه شعر و هنر کلامی استوار بوده از اینرو مردم جهان افتخارات گذشته ایران را در زمینه هنری مهمترین پشتوانه ملی ما میشناسند. برای دستیابی به پیشرفتهای دانش و فنآوری و اقتصادی و ورود به دوران آگاهی انفرماتیک، مناسب است که بنیاد هویت ملی ایران را با ستونهای پولادین خرد نیرومندتر کنیم. درجه پیشرفت کشورها در معنا و در ژرفا متناسب با کل مجموع مردم خردگرا و میزان متوسط خردگرایی آن کشور است.
سمینار اسطرلاب شناسی (کارگاه اسطرلاب)
پروفسور هوخندایک
خانه ریاضیات اصفهان 29 اردیبهشت 1378
“شناساندن اسطرلاب و نحوه استفاده از آن از روی یک نمونه ساخته شده”
اسطرلاب یک نام یونانی و متشکل از دو کامه اسطر به معنای ستاره و لاب به معنای گرفتن است که معنای اصلی آن گرفتن اطلاعات از ستارگان است.
در این کارگاه علاوه بر معرفی اجزای اسطرلاب و نحوه ساخت یک اسطرلاب ساده، تعدادی از کاربردهای آن نیز آموزش داده شد. این کاربردها عبارتند از :
اندازهگیری زمان : با اسطرلاب در کل دوره شبانهروز میتوان فهمید چقدر از زمان طلوع خورشید گذشته است یا چقدر به آن مانده است. همین کار برای ظهر شرعی و غروب آفتاب نیز قابل انجام است.
تشخیص جهات اصلی جغرافیایی
تعیین قبله (جهت مکه) در هر نقطه از زمین با دانستن اعتلاف عرض جغرافیایی آن نقطه با مکه
طالع بینی: موقعی که به عنوان طالع افراد شناخته میشود، بر روی اسطرلاب همان موقعی است که هنگام تولد وی از افق بالا میآید.
ریاضیات و منطق
روز شنبه پس از سخنرانی پروفسور عنایت و راس ساعت 6 بعدازظهر، سخنرانی پروفسور وانانن استاد دانشگاه هلسینکی فنلاند با موضوع: “ریاضیات و منطق” در خانه ریاضیات اصفهان برگزار خواهد شد.
زمینههای تحقیق پروفسور وانانن:
مبانی ریاضی، منطق در علوم کامپیوتر
منطق محض،
تئوری مدلسازی، نظریه مجموعهها
خیام و هندسههای نااقلیدسی
دکتر جعفر آقایانی چاوشی
مرکز تحقیقات صائب
هندسههای نااقلیدسی گرچه در قرن نوزدهم بوسیله لوباچفسکی و ریمان کشف شدند، اما این دو ریاضیدان و ریاضیدانان دیگری که به نحوی در این کشف سهیم بودهاند، مستقیم و یا غیرمستفیم متأثر از نظریات حکیم امر خیام بودهاند. در این گفتار پس از بررسی رساله خیام درباره اصل موضوع پنجم اقلیدس (اصل خطوط متوازی) ارتباط آن با هندسههای نااقلیدسی مورد تحقیق قرار گرفته و آنگاه تأثیر آن بر دانشمندان پس از وی نشان داده شده است.
گزیدهای از سخنرانی پروفسور هوخندایک
همانطور که در بخش قبل اشاره شد سخنرانی پروفسور هوخندایک درباره ریاضیات ایرانی قرون سوم تا نهم هجری و ارتباط آن با ریاضیات هلند در قرون شانزده و هفده میلادی بود، در ابتدای سخنرانی پروفسورهوخندایک به این اشاره کرد که شکوفایی ریاضیات دوره اسلامی در قرون 3 تا 9 هجری بوده است، اما این دوران برای ریاضیات هلند در قرون 16 و17 میلادی بود، و اهمیت این دوران از سوی دیگر به این دلیل نیز بود که علاوه بر منابع لاتین ، برای اولین بار برخی منابع به زبان هلندی هم ترجمه شد.
سپس وی اشاره نمود که مقایسه ریاضیات اسلامی و پیشرفت آن در ایران و هلند نشان می دهد که خیلی از مطالب با یک فاصله حدود دو قرن و به موازات هم اما کاملا مستقل انجام شده اند،از جمله محاسبه عدد پی یا به کار بردن کسرهای اعشاری در محاسبات ریاضی.
و در ادامه به شباهت های موجود بین این مطالعات پرداخت ، مثل استفاده از چند ضلعی ها در محاسبه عدد پی .
پروفسور هوخندایک در ادامه صحبت های خود اظهار داشت که در ضمن مطالعه آثارریاضیدانان هلندی و یا ترجمه هلندی آثار دیگر ریاضیدانان ،به نام ریاضیدانان ایرانی برخورده است ،مثل کتاب ترجمه اصول اقلیدس به زبان هلندی ،که در آن مسأله ای از اقلیدس توسط ابوسهل کوهی ریاضیدان ایرانی تعمیم داده شده است.
مسأله در ابتدا این بوده :
.jpg) که ثابت می شود مساحت دو دایره سبز رنگ با هم برابر است.
که ثابت می شود مساحت دو دایره سبز رنگ با هم برابر است.
تعمیم ابوسهل کوهی به این صورت بود که:
که باز هم ثابت می شود مساحت دو دایره سبز رنگ با هم برابر است.
البته مترجم هلندی در بخشی از مسأله تصحیح هایی روی محاسبات ابوسهل انجام داده است.
در ادامه هوخندایک به وجود نسخ خطی گرانبها و منحصر بفردی از آثارریاضیدانان ایرانی ،که توسط ریاضیدان هلندی یاکوبس خولیوس به هلند برده شده بود ، اشاره کرد و اضافه نمود که این نسخ خطی علاوه بر ارزش علمی به خاطر اینکه نشان دهنده نقش موثر دانشمندان ایرانی در روند رشد ریاضیات است ،از اهمیت ویژای برخورمی باشند.
وی در بخش دیگری از سخنان خود به مسأله یافتن اندازه ضلع چهارم از چهارضلعی که اندازه سه ضلع دیگر و مساحت آن مشخص است اشاره کرد و اظهار داشت که جواب این مسأله ، از حل یک معادله درجه چهارم به دست می آید و ریاضیدانان ایرانی این گونه معادلات را از طریق مقاطع مخروطی حل می کردند، در حالی که این نکته از نظر مترجم هلندی پنهان مانده بود و او اساسا متوجه این مطلب نشده بود.
در پایان پروفسور هوخندایک از صحبت های خود این گونه نتیجه گیری کرد که :
علاقه و توجه به ریاضیات ایرانی از دیرباز درمیان ریاضیدانان هلندی وجود داشته است و همین علاقه موجب حفظ برخی از آثار مهم ریاضیدانان ایرانی گردیده است .و دیگر اینکه، همانگونه که مستندات مقاله ارائه شده نشان می دهد ریاضیات می تواند به عنوان پلی بین فرهنگ ها عمل نماید.
نهمین گردهمایی جامعه آزاد رایانش ابری اصفهان
پنجشنبه 4 شهریور 1395
ساعت 16:30 الی 19
سالن همایش میرزاخانی، خانه ریاضیات اصفهان
هفتمین گردهمایی جامعه آزاد رایانش ابری اصفهان
پنجشنبه 3 تیر 1395، ساعت 16:30 الی 19
Mathematical activities for young students
Christian MAUDUIT
Professor of Mathematics
شنبه 8 خرداد 1395، ساعت 17
فایل سخنرانی
چکیده : توضیح بسیاری از مفاهیمی که ما تدریس می کنیم ناشی از فرایند تاریخی دراز مدتی است که مدت زمان طولانی حتی قرنها را به خود اختصاص داده است. فرایند اکتساب نیازمند فائق آمدن بر موانعی است که بتواند از اینگونه موانع دانش شناختی عبور کند. اغلب اوقات یک سخنرانی علیرغم داشتن کیفیتش، هیچوقت مشکلات عمقیش را نمیتواند بیان کند. حال باید دید چه اقدام موازی در این راستا میتوان انجام داد که این نقیصه را جبران کند و کدام بخش در این مناظره علمی، پیرامون تحقیقات ریاضی در این جهت نقش ایفا میکند. هدف از این گفتگو، ارائه تجربیات مبتکرانه آموزشی برای دانشآموزان مدارس، دبیرستان و دانشجویان براساس فعالیتهای تحقیقاتی ریاضی را شکل میدهد.
ششمین گردهمایی جامعه آزاد رایانش ابری اصفهان
زمان: 6 خرداد 1395، ساعت : 16:30 الی 19
مقایسه محاسبات در شهر رم با استفاده از سنگریزه و در ایران با استفاده از ماسه
کارگاه عملی با چشماندازی تاریخی
Wilfred de Graaf and Tom Reijngoudt
Mathematics Department, Utrecht University
شنبه 11 اردیبهشت 1395، ساعت 17
چکیده :
در اوایل قرون وسطی، محاسبات در اروپای غربی، با استفاده از وسایلی توسط ریگها، بر روی صفحهای محاسبهگر و با استفاده از سیستمی باستانی(کهن)، اختراع شد. در سالهای 1000 تا 1200 سیستم محاسبه با استفاده از ماسهها در سیستم اعشاری، که توسط خوارزمی ریاضیدان ایرانی، بسط و توسعه داده شده، در اروپا به شهرت رسید. (این اثر خوارزمی در ترجمههای متون عربی مفقود گردید و تنها در ترجمههای لاتین قرون وسطی باقی ماند). در اواخر قرون وسطی و عهد رونسانس، هر دو سیستم ماسه و ریگ در اروپای غربی مورد استفاده قرار گرفت که از مواد متفاوت استفاده میشده یعنی بجای ماسه از کاغذ و به جای ریگها از سکهها استفاده میشده است.
در این کارگاه عملی، شرکتکنندگان تلاش خود را در راستای انجام محاسبات به کار میبرند (از قبیل عمل جمع، ضرب و جذر) که با استفاده از وسایل معتبر و تایید شده در هر دو سیستم، این دو روش صورت میگیرد و سپس شرکتکنندگان این دو سیستم را با تجربه شخصی خود مقایسه میکنند. جنبههای تعلیمی و دانش شناختی این گونه فعالیتها، میتواند عموما مورد بحث و تبادل نظر قرار گیرد.
Combinatorics and geometry of random tilings from microscopic to macroscopic scales
سخنران : سدریک بوتیلیر
پنجشنبه 9 اردیبهشت 1395
Non-Linear Dimensionality Reduction by Isometric Patch Alignment
چهارشنبه، 8 اردیبهشت 1395، ساعت 17
پروفسور علی قدسی
دانشکده آمار و علوم آماری، دانشگاه واترلو
Abstract: We propose a novel dimensionality reduction method which has low computational cost. This method is inspired by two key observations: (i) the structure of reasonably large patchesof high-dimensional data can be preserved as a whole, rather than divided into small neighborhoods; and (ii) attaching two neighboring patches will align them such that the overall rank does not increase. In the proposed approach, first the data is clustered, so that it is conceptually reduced to a set of overlapping low-rank clusters. Each cluster is embedded into a low-dimensional patch and then all of the patches are rearranged such that their border points are matched. We show that the rearrangement can be computed by solving a relatively small semide nite program. The embedding computed by this optimization is provably low-rank. The proposed method is stable, fast and scalable; experimental results demonstrate its capability for manifold learning, data visualization, and even complex tasks such as protein structure determination.
پنجمین گردهمایی جامعه آزاد رایانش ابری اصفهان
زمان: 9 اردیبهشت 1395، ساعت : 16:30 تا 19:30
جامعه آزاد رایانش ابری اصفهان با همکاری بخش دانشجویی خانه ریاضیات استان اصفهان برگزار میکند:
برنامههای مراسم :
- آغاز مراسم با ارائه گزارشی از جلسات پیشین
- سمینار اول: Mobile Cloud Computing
- ارائهدهنده: خانم مهندس شادی ترابی
- سمینار دوم: CloudIOT
- ارائهدهنده: خانم مهندس شادی ترابی
- پذیرایی و شبکهسازی
- پرسش و پاسخ
با حضور آقای دکتر مرتضی سرگلزایی جوان از دانشگاه صنعتی امیرکبیر
چرا به کودکان دبستانی ریاضیات آموزش داده میشود؟
طغیان انگشتری
شنبه، 4 اردیبهشت 1395، ساعت 16
این سؤال پرسش کلیدی است چرا که پاسخ مستدل و مجاب کننده به آن میتواند در زمینهی آموزش کودکان راهگشا باشد.
به منظور ارائهی پاسخ قطعی به این پرسش اساسی، در وهله اول بایستی در مورد سه مفهوم کودکان دبستانی، آموزش و ریاضیات به یک وحدت نظر علمی و مستند دست یابیم. پس از آن، امکان توافق در مورد پاسخ بدست آمده بیشتر خواهد بود. نشان داده خواهد شد که آموزش ریاضیات (و نه صرفا آموزش حساب و هندسه) میتواند نقشی بسیار راهگشا و بیبدیل را، در ارتقا سطح آموزش و رشد آگاهی عمومی کودکان بر عهده گیرد. همراه با آن، شیوه روز آمد آموزش ریاضیات به کودکان نیز آشکار خواهد شد.
بخش اول
کودک دبستانی کیست؟
مشکلات رفتاری با آنان کدامست؟
با کودکان دبستانی چگونه باید رفتار نمود؟
معماری و موسیقی
سخنرانان: فریدون فراهانی
پنجشنبه 6 اسفند 1394، ساعت 17
مباحث نظری و مصداقهای عملی درباره پیوند معماری و موسیقی را میتوان دارای عمری تا زمان یونان باستان و فلاسفه پیش از سقراط مانند تالس، آناکسیماندر و آناکسیمنس در سدههای هفتم و هشتم پیش از میلاد دانست که برای کشف معیار و قانونی برای زیبایی و کمال هنر، دستاوردهای عددی ریاضی و تناسبات هندسی را به معماری و موسیقی تعمیم دادند. این آغاز راهی بود که فیثاغورث و پیروانش به مقصد رساندند. در دورانهای مختلف تاریخ هنر نیز از پیوند و همانندی معماری و موسیقی، بارها سخن به میان آمد که دوران رمانتیک و اوایل قران بیستم نمونههای شاخص آن به شمار میآیند. در روزگار ما نیز بررسی ارتباط و همانندی هنرهای مختلف، یکی از مهمترین مباحث در پژوهشهای تخصصی به شمار میآیند که همانندی معماری و موسیقی، نیز با توجه به پیشینه آن در تاریخ، میتواند شناخت بهتری از هریک به دست دهد.
مهمترین دستاورد این دیدگاهها تاکید بر این بود که در میان هنرها، معماری و موسیقی همواره بیانی انتزاعی دارند و هریک روشی مشابه در تجلی خود برمیگزینند. معماری در بستر مکان، با عناصر بصری و موسیقی در بستر زمان، با عناصر شنیداری، هر دو بهدور از صُوَر عینی و قراردادی تنها نسبتهای ریاضی را تجسم میبخشند.
این موضوع را از زاویه دید، تجربه حسی رویاورویی با فضای معماری و موسیقی، نیز میتوان توصیف کرد: حرکت انسان در فضای معماری، احساسات ذهنی برآمده از کیفیت عناصر معماری و ویژگیهای مکان را در او میآفریند. به همین شیوه حرکت نتهای موسیقی نیز، در گوش انسان بازهم فضایی ذهنی ایجاد میکند که برآمده از چگونگی ترکیب عناصر موسیقایی در بستر زمان است.
سمینار عکاسی
سخنرانان: شیوا انصاری پورو امیر کیان ارثی
چهارشنبه 5 اسفند 1394، ساعت 17
معرفی اجمالی علم – هنر عکاسی
تاریخچه عکاسی
اولین ابزارهای ثبت تصویر
تیپولوژی آثار عکس در جهان (مفاهیم و نمونه ها)
APPLIED
SOCIAL
DOCUMENTARY
COMMERCIAL
FINE ART
آشنایی با هنرمندان عکاس مشهور ایرانی
آشنایی با عکاسان حرفهای غیر ایرانی
تفاوت بین عکاسی دیجیتال و فیلم
معرفی منابع
چهارمین جلسه جامعه آزاد رایانش ابری
با همکاری بخش دانشجویی خانه ریاضیات اصفهان
پنجشنبه 8 بهمن 1394، ساعت 16 الی 19
The Idea of
Parrallel Processing
سروش حاج زرگر باشی
پنجشنبه 26 آذر 1394، ساعت 17
در این سمینار ابتدا انگیزه استفاده از پردازش موازی برای حل مسائل بیان شده، سپس به بیان مفاهیم کلی و تعاریف در این علم میپردازیم. در ادامه، پس از بیان مختصری از الگوهای پردازش موازی، ابزارهای مختلف و الگوها را مورد بررسی قرار میدهیم. برای روشنتر شدن بحث چند مثال از استفاده از ابزار موازی سازی نیز مطرح خواهد شد. این سمینار به منزله بیان مقدمات پردازش موازی بوده و دانش اولیه مورد نیاز برای این سمینار، برنامهنویسی و دانش جزیی در سازمان کامپیوتر میباشد.
معماری بستک
مهندس فریدون فراهانی
استاد دانشگاه هنر اصفهان
چهارشنبه 25 آذر 1394، ساعت 17
شهر بستک در جنوب ایران و در فاصلهای نزدیک به بندر لنگه، در زمانهای نه چندان دور، نقش مهمی در فرهنگ کرانههای خلیج فارس داشت. اهمیت فرهنگی، مذهبی و بازرگانی آن در سدههای گذشته، نوعی نقش مرکزی برای این شهر در منطقه ایجاد نمود و معماران این شهر با حضور در مناطق پیرامون، شیوه معماری خود را فراتر از محدوده بستک، تا بندر لنگه و بسیاری از کرانههای شمالی و جزایر خلیج فارس گسترش دادند. از سال 1890 م. به بعد، و هم زمان با مهاجرت گسترده بازرگانان بستکی ایران به دوبی، محلهای به نام برای سکونت آنان، به دست معماران بستکی بنا شد و به یاد بستک ایران، بستکیه نام گرفت. این محله اگرچه به عنوان میراث فرهنگی دوبی، در تبلیغات دولتی امارات معرفی میشود، اما بنا به شواهد ارائه شده در این پژوهش، نمونه آشکاری از خلاقیت و هنر معماران بستکی در کرانههای جنوبی خلیج فارس است. افزون بر اینکه ردپای تاثیر معماری بستکی در آنسوی خلیج فارس، تنها محدود به بستکیه دوبی نیست و باید شیوه معماری بستکی به عنوان سبکی فراگیر و مهم در دو سوی خلیج فارس یاد کرد.
دومین گردهمایی جامعه آزاد رایانش ابری اصفهان
با حضور آقای دکتر مرتضی سرگلزایی جوان از دانشگاه صنعتی امیرکبیر
پنجشنبه 5 آذر 1394
ساعت 16 الی 19:30
برنامههای مراسم:
سمینار: Decentralized Cloud Storage –>> Cloud Shared By The Community (زمان: ۲۰ دقیقه)
ارائه توسط: آقای مهندس علیرضا نوری
کارگاه: مجازیسازی با vSphere (زمان ۱:۱۵ دقیقه)
ارائه توسط: آقای مهندس آرمان حفیظی
پذیرایی (زمان: ۱۵ دقیقه)
شبکهسازی/ پرسش و پاسخ (زمان: ۱:۱۵ دقیقه)
پ.ن۱. دوستانی که تمایل دارند در کارگاه به صورت عملی با سیستم شخصی خود کار کنند لپتاپ به همراه داشته باشند.
حداقل نیازمندیهای سیستمی مورد نیاز برای اجرای برنامه:
CPU: Core i5
RAM: 8 GIG
اینرسی و انرژی ماتریسهای فاصله در برخی از گرافها
سخنران: حانم شهره معراجپور
پنجشنبه 21 آبان 1394، ساعت 17:30
اولین گردهمایی جامعه آزاد رایانش ابری
با همکاری بخش دانشجویی خانه ریاضیات اصفهان
پنجشنبه 7 آبان 1394، ساعت 16
THE POWER OF NAMES IN CULTURE AND MATHEMATICS
سخنرانی آقای پروفسور لورن گراهام و آقای پروفسور کانتور
Massachusetts Institute of Technology(MIT)I
Cambridge, Massachusetts
چهارشنبه 6 آبان 1394، ساعت 17 تا 18:15
A common cencept in history is that knowing the name of something or someone gives one power over that thing or person. This concept occurs in many different forms in numerous cultures – accient and primitive tribes, Islam, Judaism, and in Egyption, Vedic Hind, and Christian traditions. Some writers find it embedded in the first verses of Genesis, written probably over three thousand years ago; other believe it to be an intrinsic characteristic of classical Greek religion; still other find it a central feature in magic and folklore, and modern feminist writers often see it as the reason that a woman in marriage is often asked to take the name of her new husband. In all these cases “naming” something or someone is seen as the exertion of dominion over that thing or person. Iwill give examples of some of these, and then I will proceed to the role of “naming” in the twentieth century mathematics and maintain that not only has it been central, but that it played an important role in the creation of the famous Moscow School of Mathematics.I
گروهی خوانی مقاله
On proof and progress in mathematics
مقاله
By Willian P. Thurston
پنجشنبه 28 آبان 1394، ساعت 17:30
نویسنده این مقاله ویلیام ترستن ریاضیدان پرآوازه آمریکاییست که به خاطر دست آوردهای قابل توجه و انقلابی اش در فهم خمینهها در 1982 برنده مدال فیلدز شد. او همچنین خالق حدس معروف هندسه سازی است که در 2002-2003 اثبات شد. این مقاله به نوعی تجربه شخصی از ریاضی ورزیدن یکی از انقلابی ترین ریاضیدانان معاصر است که به زبانی نسبتا ساده و شیوا حتی برای غیر ریاضیدانان نوشته شده که یکی از مقالات معروف درباره ریاضی ورزی و توصیف کار ریاضی ( تا فهم در سطح درجه یک و در مرزهای محکم ریاضی) است.
THE FOUR A’S OF AMERICAN EDUCATION
خانم پروفسور پاتریشیا گراهام
Harvard University, Cambridge, Massachusetts
چهارشنبه 6 آبان 1394، ساعت 18:30 الی 19:15
My “Four A’s” talk comes in two parts that can either be given separately depending on the audience’ interest. The “Four A’s” are the aspirations that Americans have had for their educational institution -school and universities- over the twentieth and now twenty-first centuries. My talk argues that each of these aspirations was warranted at the time, each was achieved to a considerable degree, and each changed to a new aspiration after three decadesor so.
تشخیص بیماریها با استفاده از آنالیز چشم انسان
آقای مهرداد ایزدی
دانشجوی مهندسی پزشکی
پنج شنبه 30 مهر 1394، ساعت 17
بهبود کران بالا برای نرخ اطلاعاتِ طرحهای تقسیم راز القا شده
بهوسیله واموس ماتروید
آسیه شفیعی
دانشکده ریاضی و کامپیوتر خوانسار
پنجشنبه 16 مهر 1394، ساعت 17
چکیده:
طرح تقسیم راز یک پروتکل است که توسط آن یک واسطه سهمهایی از یک راز را بین مجموعهای از شرکاء بهگونهای تقسیم میکند که زیرمجموعههای مجاز با به اشتراک گذاشتن سهمهایشان قادر به بازسازی راز باشند ولی زیرمجموعههای ممنوع حتی با به اشتراک گذاشتن سهمهایشان نیز، هیچ اطلاعاتی از راز بهدست نیاورند. کارایی یک طرح تقسیم راز از نقطه نظر نرخ اطلاعات بررسی میشود. طرح تقسیم راز با نرخ اطلاعات برابر یک را ایدهآل مینامند. نرخ اطلاعات یک ساختار دسترسی، کوچکترین کران بالایِ نرخ اطلاعات روی تمام طرحهای تقسیم راز مرتبط با ساختار دسترسی است. ردهبندی ساختارهای دسترسی ایدهآل یک مسئله حل نشده در بحث تقسیم راز است. بریکل و داونپورت نشان دادند که هر طرح ایدهآل بایستی از روی یک ماتروید بهدست آید. پادرو و همکارش ثابت کردند که هر ساختار دسترسی با نرخ اطلاعات بزرگتر از باید بهوسیله یک ماتروید القا شده باشد. مسئله ردهبندی ساختارهای دسترسی ایدهآل همچنان حل نشده باقی مانده و باعث ایجاد مسئله حل نشده یافتن نرخ اطلاعات برای ساختارهای دسترسی القا شده بهوسیله ماترویدهای غیرقابل نمایش شده است.
در این سمینار نحوه القا شدن یک ساختار دسترسی بهوسیلهی یک ماتروید را نشان میدهیم. سپس به دلیل سه ویژگی خاص واموس ماتروید و ناشناخته بودن کران بالای ساختارهای دسترسی القا شده بهوسیلهی واموس ماتروید، به بررسی کران بالای نرخ اطلاعات این ساختارها میپردازیم. سه ویژگی خاص واموس ماتروید عبارتند از :
واموس ماتروید کمینه مثال شناخته شده مثال کمینه در بین ماترویدهای غیرقابل نمایش است.
اولین مثال شناخته شده از یک ماتروید است که پذیرای طرحهای ایدهآل نیست.
اولین مثال شناخته شده از ساختارهای دسترسی با نرخ اطلاعاتی اکیداً بزرگتر از است
طرحهای تقسیم راز چندبخشی ایدهآل
منصوره باقری
دانشکده ریاضی و کامپیوتر خوانسار
پنجشنبه 16 مهر 1394، ساعت 18
چکیده:
در طرحهای تقسیم راز چندبخشی سهامداران به چند بخش تقسیم میشوند و همهی سهامداران در یک بخش نقشهای یکسانی دارند. در این سمینار، دستهبندی تمام ساختارهای دسترسی چندبخشی ایدهآل بهطور کلی مورد بررسی قرار گرفته است. این سمینار بر اساس ارتباط معروف بین طرح تقسیم راز ایدهآل و ماتریدها میباشد و همچنین مقدماتی از یک ساختار ترکیباتی جدید در طرح تقسیم راز بهنام پلیماترید مورد بررسی قرار میگیرد. ابتدا دستهبندی ماتریدپرتهای چندبخشی از دیدگاه پلیماتریدهای صحیح مورد بررسی قرار میگیرد. به عنوان نتیجهای از این دستهبندی، یک شرط لازم برای اینکه یک ساختار دسترسی چندبخشی ایدهآل باشد، ارائه خواهد شد. در ادامه نمایش پلیماتریدهای صحیح با استفاده از مجموعه زیرفضاهای برداری بکار گرفته شده، تا دستهبندی از ماتریدهای چندبخشی نمایشپذیر ارائه گردد و یک شرط لازم و کافی برای اینکه یک ساختار دسترسی چندبخشی، ایدهآل باشد، ارائه میگردد و همچنین چارچوب یکپارچه جهت مطالعه مسائل حل نشده راجع به تأثیر ساختارهای تقسیم راز چندبخشی ایدهآل بیان میشود. در نهایت نتایج عمومی به دست آمده را بهکار برده تا یک دستهبندی کاملی از ساختارهای دسترسی سهبخشی ایدهآل ارائه گردد که تاکنون به عنوان یک مسأله حل نشده شناخته میشد.
Are all aperiodic tilings substitutive ?
Thierry Monteil
یکشنبه 22 شهریور 1394، ساعت 17
Abstract : A tile set is a finite set of polygons where each edge have a color. A tile set T tiles the plane if the plane can be covered by translated copies of elements of T, where two adjacent edges must have the same color. A tile set is aperiodic if it tiles the plane, but if this can not be done in a periodic way. Most aperiodic tilings are obtained from a substitution process (Penrose, Ammann-Beenker, Robinson,…). We introduce two invariants to quantify the level of aperiodicity of a tile set. One is topological, the other is metric. They both rely on the way a tile set tile can tile other objects than the plane. Those invariants allow to prove that the tile sets of Kari and Culik are not ruled by a substitution process.g
An Introduction to Sage Mathematics Software System
Thierry Monteil
دوشنبه 23 شهریور 1394 ساعت 16
Abstract : Sage is a free open-source mathematics software system licensed under the GNU Public License (GPL). It combines the power of about 100 open-source packages with a large amount of new code to provide a free open source platform for mathematical computation. Sage has many notable features like using Python as the main language, being free and open-source, online and cloud availability, etc.I
Sage is a powerful software system with functionality in different areas of mathematics including: Algebra, Geometry, Number Theory, Calculus, Group Theory, Linear Algebra, Combinatorics, Numerical Computations, etc.g
In this seminar/workshop, there will be a talk about Sage software system and there will be a tour of a number of Sage features. Also, participants are guided through doing a few example practices by using Sage
فلسفه منطق و منطق فلسفی
سمینار توسط آقای حمید اعلایینژاد
پنجشنبه 15 مرداد 1394، از ساعت 17
آشنایی مقدماتی با نظریه موجکها
توسط خانم مینا ترابی
دانشجوی دکترای ریاضی
پنجشنبه 24 اردیبهشت 1394، ساعت 10
چکیده :
موجک تابع مشخصی است که بسط توابع دیگر بر اساس انتقالها و اتساعهای آن انجام میگیرد. امروزه نظریهی جدید موجکها جایگزین نظریههای کلاسیک از جمله روش کلاسیک نظریه فوریه برای حل مسائل مختلف کاربردی در زلزله شناسی، پردازش سیگنالها در سیستمهای مخابرات، پردازش تصویر و بینایی کامپیوتر، ذرات بنیادی و کوانتوم مکانیک، نظریه تقریب و مکان یابی، ژنتیک و فیزیک شده است. این نظریه جدیدی کاربردی ریاضیات یکی از مؤثرترین پل ارتباط علم ریاضیات نظری به عملی است.
Segment Trace: A Probabilistic Based Approach For
Segmenting Execution Traces Into Distinct Execution Phases
سمینار توسط آقای محمدرضا رجالی
دوشنبه 94 مرداد 5 ، ساعت 17


Challenges in Processing of the Intracardiac Electrogram During Surgery for Atrial Fibrillation
سمینار توسط آقای دکتر سعید گازر
دانشگاه Queen’s
پنجشنبه 25 تیر 1394، ساعت 17
In this seminar we present a summary of the mechanic of human heart and describe Atrial Fibrillation which is a major heart disease. We then give some idea about af surgery and about our current research and unsolved challenges on the signal processing and the state of technology for treatment of af via ablation.i
کارگاه معرفی موجک و کاربردهای آن
توسط خانم دکتر آسیه ابراهیم زاده
پنجشنبه 22 مرداد 1394
ساعت 16 الی 20
مطالبی که در کارگاه ارائه میشود، میتوان به صورت زیر طبقهبندی کرد :
از تبدیل فوریه تا تبدیل موجک
تاریخچه پیدایش موجک
مقدمهایی بر تئوری موجک
کاربردهای موجک در علوم مختلف
آشنایی با جعبه ابزار موجک در نرم افزار متلب
ریاضیات پشت پردهی ساز یا چطور پردههای ساز را مرتب کنیم؟
توسط آقای بردیا حسام
17 اردیبهشت 1394
ساعت 17
چکیده:
موسیقی، از گذشتههای دور به دو شاخهی عملی و نظری تقسیم میشده است. در بخش عملی، بیشتر به مسئلهی اجرای موسیقی (بهعنوان شکل طبیعی بروز موسیقی) پرداخته میشد و در بخش نظری، به پشتوانههای اجرا از قبیل چرایی و چگونگی صداهای درست. آن بخش از موسیقی نظری که در آن به اصوات و نسبت فواصل آنها میپرداختهاند، همواره شاخهای از ریاضیات به حساب میآمده و اغلب حکما و فلاسفهی قدیم، در کنار بحثهای مربوط به چرایی و چگونگی تولید اصوات و کارکرد و جایگاه موسیقی، نگاهی هم به موسیقی و مسئلهی فاصلههای مطلوب و نامطلوب داشتند.
در این صحبت کوتاه، میخواهیم به توصیفی تجربی از چگونگی عملکرد «تار مرتعش» برسیم. برپایهی این توصیف و کمی ضرب و تقسیم، نظام حاکم بر فاصلههای پردههای سازها را «کشف» میکنیم و درستی کشفمان را بررسی میکنیم!
پروتز چشم
مهرداد ایزدی
دانشجوی مهندسی پزشکی
27 فروردین 1394 ساعت 17:30
تخمین همزمان و شگفتیهای ابعاد بالا
دكتر كسری علیشاهی
عضو هئیت علمی دانشگاه صنعتی شریف
همراه با معرفی خانه ریاضیات اصفهان با حضور آقای دكتر علی رجالی
چهارشنبه 20 اسفند 1393 ساعت 14 الی 16
دانشگاه صنعتی اصفهان دانشكده علوم ریاضی سالن خوارزمی
چالشهای صنعت، فرصتهای علوم کامپیوتر
همراه با معرفی بخش دانشجویی خانه ریاضیات اصفهان
یکشنبه 17 اسفند، ساعت 14 الی 16
مکان: دانشکده ریاضی دانشگاه اصفهان
سخنران: علیرضا حق شناس
کرانهای جدید روی میانگین نرخ اطلاعات طرحهای تقسیم راز برای ساختارهای دسترسی
آستانه وزن دار بر پایه گراف
خانم مریم براتی
دانشجوی فوق لیسانس رمزنگاری دانشگاه اصفهان واحد خوانسار
پنج شنبه 14 اسفند 1393 ساعت 15
چکیده :
یک طرح تقسیم راز، یک پروتکل است که در آن شخصی به نام واسطه، سهمهایی از یک کلید مخفی را از بین یک مجموعه n تایی از سهام داران توزیع میکند به طوریکه فقط زیرمجموعههای مجاز از سهام داران میتوانند با سهمهای دریافتیشان کلید مخفی را بازسازی کنند، درحالی که زیرمجموعههای غیرمجاز هیچ اطلاعاتی درمورد کلید مخفی ندارند. مجموعهی تمام زیر مجموعههای مجاز، ساختار دسترسی این طرح نامیده میشود. نرخ اطلاعات (میانگین نرخ اطلاعات) یک طرح تقسیم راز، نسبت اندازهی کلید مخفی به بیشینهی اندازهی (میانگین اندازه) سهمها است. در یک طرح آستانه وزن دار، به هر سهام دار یک وزن نسبت داده می شود. یک زیرمجموعه، مجاز است اگر و فقط اگر مجموع وزنهای سهام داران آن کمتر از مقدار آستانهی مفروض نباشد. موریلو و همکارانش طر حهایی برای ساختار دسترسی آستانه وزن دار مطرح کردند و آنها را
-Kگرافهای وز ن دار نمایش دادند. آنها این نوع از ساختارهای دسترسی را به طور کامل مشخص کردند و به نتیجهای درمورد نرخ اطلاعات دست یافتند. در این سمینار میانگین نرخ اطلاعات طرحهای تقسیم راز برای این گونه ساختارها بررسی خواهد شد. همچنین دو ساختار پیچیده مطرح میشود که هرکدام از آنها مزایای خاص خود را دارند. از طرفی هر دوی آنها برای n/k های بزرگ نتایج بسیار خوبی از خود نشان میدهند.
امضاهای انکارناپذیر فاقد گواهی با استفاده از نگاشتهای دوخطی
خانم زهرا ملک
دانشجوی کارشناسی ارشد رمزنگاری از دانشگاه اصفهان واحد خوانسار
پنج شنبه 14 اسفند 1393 ساعت 16
چکیده
سیستمهای رمزنگاری کلید عمومی فاقد گواهی از مسائل کلید اصلی اسکرو درهویت، براساس سیستمهای رمزنگاری کلید عمومی اجتناب میکنند و به گواهیهای پرهزینه در زیر ساختهای کلید عمومی نیازی ندارند. این اصول رمزنگاری نکات عمده ای را مطرح کرده است و در سالهای گذشته بسیاری از طرحهای فاقد گواهی مطرح شده است. در این سمینار یک طرح امضای انکارناپذیر فاقد گواهی بر پایه نگاشتهای دوخطی معرفی خواهد شد. برای تحلیل امنیت طرح ارائه شده، مفاهیم امنیتی از امضاهای انکارناپذیر را در زیر ساخت های کلید عمومی کلاسیک به منظور فاقد گواهی بودن آنها توسعه میدهیم. براساس روشهای امنیتی که به صورت رسمی تعریف شده اند، نشان خواهیم داد که طرح ارائه شده در تمام خواص امنیتی تحت استانداردهای مشخص در مدل غیبگوی تصادفی صدق میکند. در مقایسه با امضاهای انکارناپذیر فاقد گواهی موجود، این امضای معرفی شده مؤثرتر میباشد. ضعف طرح ارائه شده که همان میزان جعل ناپذیری مطرح است در یک روش ضعیف اثبات شده است.
مروری بر ساختار و دینامیک شبکههای پیچیده
دکتر کیوان آقابابائی
پنج شنبه 2 بهمن 1393 ساعت 16
چکیده :
در سالهای اخیر موضوع «شبکههای پیچیده» کاربرد وسیعی در علوم مختلف از جامعهشناسی و علوم زیستی گرفته تا مهندسی ارتباطات و اقتصاد یافته است. بسیاری از ساختارهای پیچیده را میتوان با شبکههای پیچیده مدل کرد. شناخت ساختار و کارکرد این شبکهها و درک ارتباط میان ساختار و دینامیک شبکهها از موضوعاتی است که در سالهای اخیر بسیار مورد توجه پژوهشگران حوزههای مختلف علم و فناوری قرار گرفته است. ابزار ریاضی اساسی در مطالعهی شبکههای پیچیده نظریهی گراف است. در این سخنرانی ضمن مرور مختصری بر کاربردهای شبکههای پیچیده، برخی مدلهای مهم شبکه را از نظر میگذرانیم و چند فرایند دینامیکی مرتبط با آنها را مرور میکنیم.
روایتی دیگر از خوان ششم رستم و
کاربرد گل آفتابگردان در علوم کامپیوتر
پنج شنبه 4 دی 1393، ساعت 16:30
نوید نصر اصفهانی
ارژنگ دیو، کیکاووس و n-2 نفر از لشکریان وی را به بند انداخت. هنگامی که رستم برای آزاد کردن ایشان به مازندران رسید، دیو، آزادی رستم، کیکاووس و لشکریان را منوط به شرط زیر کرد :
هر یک از n نفر را در دخمهای در بسته و بدون پنجره زندانی کند و دیو به هر ترتیبی که خواست، تک تک ایشان را، یکی یکی، به دشتی با بینهایت صندوقچه در بسته ببرد که در هر صندوقچه سنگیست، یک روی سپید و روی دیگر سیاه. هربار، کسی که به دشت برده شده اجازه دارد به سراغ حداکثر 10loglogn صندوقچه رفته سنگ درون آن را نگاه کرده و درصورت تمایل آن را بچرخاند و سپس به دخمه خود باز گردانده شود. او قول داده که اگر تک تک افراد در هنگام بازگشت از دشت به دخمه خود، بتوانند تشخیص دهند که آیا نفر nام بوده اند یا خیر، همگی ایشان را آزاد کند. او همچنین به رستم اجازه داده که تا قبل از روز شروع، هر تعدادی از صندوقچهها را که میخواهد شماره گذاری کرده و در صورت تمایل سنگ درون آنها را بچرخاند.
فردا صبح قرار است رستم برای شماره گذاری و آماده کردن صندوقچهها به دشت برود. او که هم اکنون در کنار کاووس و باقی لشکریان است برای یافتن راهکاری برای نجات، به کمک شما نیاز دارد. روشی را به آنها بیاموزید که هر یک بتوانند تشخیص دهند که آیا نفر آخر هستند یا خیر.
دقت کنید که از فردا صبح هیچ یک از n نفر اجازه صحبت کردن با یکدیگر را ندارند و همدیگر را نخواهند دید. همچنین در نظر داشته باشید که دیو میتواند هر تعداد فردی را که بخواهد (جداگانه) به دشت ببرد.
مسئله فوق بیانی از مسئله Cell Probe Model است. در این سمینار با راه حلی برای این مسئله در علوم کامپیوتر آشنا خواهیم شد. سپس به کمک لم گل آفتابگردان به بیان حد پایینی برای تعداد صندوقچههایی که برای حل مسئله نیاز به باز کردن آنها داریم خواهیم پرداخت و در نهایت نگاهی خواهیم داشت به اثباتی برای لم گل آفتابگردان که توسط اردوش و رادو ارائه شده است.
سمینار معماری و موسیقی
29 آبان 1393 ساعت 17
مهندس فریدون فراهانی
استاد دانشگاه هنر اصفهان
چکیده:
در دورانهای مختلف تاریخ هنر، از پیوند و همانندی معماری و موسیقی، بارها سخن به میان آمده است. معماری و موسیقی همواره بیانی انتزاعی دارند و هریک روشی مشابه در تجلی خود برمیگزینند. معماری در بستر مکان، با عناصر بصری و موسیقی در بستر زمان، با عناصر شنیداری، هر دو به دور از صُوَر عینی و قراردادی تنها نسبتهای ریاضی را تجسم میبخشند.
این موضوع را از زاویه دید تجربه حسی رویارویی با فضای معماری و موسیقی، نیز میتوان توصیف کرد: حرکت انسان در فضای معماری، احساسات ذهنی برآمده از کیفیت عناصر معماری و ویژگیهای مکان را در او میآفریند. به همین شیوه حرکت نتهای موسیقی نیز، در گوش انسان بازهم فضایی ذهنی ایجاد میکند که بر آمده از چگونگی ترکیب عناصر موسیقایی در بستر زمان است.
بررسی سیستم آموزشی فنلاند
خانم دکتر هوشیار
1 آبان 1393
موضوعات مطرح شده در این سمینار :
ویژگیهای متمایز کننده آموزش در فلاند به لحاظ اجرایی
هدف آموزش در فنلاند
انگیزه تحصیل در میان دانشآموزان
نحوه آزمون در آموزش فنلاند
سیستم خیلی خوب طراحی شده ی آموزش معلمان در فنلاند
و ….
سمینار آشنایی با روش اجزاء محدود و تحلیل عددی یک معادله دیفرانسیل پاره ای مرتبه چهار دو بعدی
(ارتعاش یک پره پیچهدار گردان )
27مهر 1393 ساعت 17:30
امیرحسین زندی آتشبار
امروزه با پیشرفت علم و تکنولوژی و همچنین نیاز به کاهش شرایط ساده سازی برای انطباق بیشتر مسائل به مسائل واقعی، حل معادلات دیفرانسیل پیچیده یکی از مشکلات پیش روی مهندسان است.
حل تحلیلی اینگونه مسائل بسیار مشکل بوده و یا عملا غیر ممکن است. به همین جهت از روشهای عددی استفاده میشود. یکی از آن روشها روش اجزاء محدود است که در این سمینار به معرفی مقدماتی این روش پرداخته میشود و یک معادله دیفرانسیل پارهای مرتبه چهار دو بعدی (تحلیل ارتعاش آزاد پره پیچه دار گردان) به روش اجزاء محدود که توسط این روش تحلیل شده است، معرفی و بررسی به روش اجزاء محدود که توسط این روش تحلیل شده است، معرفی و بررسی خواهد شد.
سمینار با عنوان آمار و تولید
پنجشنبه 3 مهر 1393، ساعت 17:30
حمیدرضا صانعی
در این سمینار با کاربردهای متفاوت و متنوع علم آمار در زمینههای مختلف صنعت آشنا خواهیم شد. چگونگی کاربرد ابزارهای آماری در کنترل کیفیت، مهندسی، بازاریابی، تحلیل فروش و امور اقتصادی مرتبط با صنعت بررسی خواهند شد. در این سمینار خواهیم دید که چگونه روشهای ساده تا بسیار پیشرفته آماری در زمینههای ذکر شده، بطور رایج کاربرد دارند. این روشها شامل نمونهگیری، رگرسیون، آمار توصیفی، سریهای زمانی و … خواهند بود.
در اینجا بررسی خواهیم کرد که چگونه آمار میتواند روشهایی بهینه و همچنین علمی را در حل مسائل روز صنعتی ارائه دهد.
آشنایی با Game Theory
سروش حاج زرگرباشی
سه شنبه 17 تیر 1393، ساعت 17:30
چکید ه: به طور کلی Game به هر موقعیت استراتژیک گفته میشود که گاه میتواند حامل تضاد منافع باشد و گاه روحیه همکاری داشته باشد. Game Theory علمی است که به مطالعه بازیها و مدل سازی شرایط استراتژیک در قالب بازی میپردازد. در این ارائه به بررسی کلی نظریه بازیها پرداخته و سعی در انتقال یک دید کلی از آن خواهیم داشت. مفاهیمی از جمله تعادل Nash و تابع Best Response را در فضای استراتژیهای خالص بیان خواهیم کرد. علاوه بر آن به تحلیل چند نمونه از کاربردهای این شاخه مهم علم ریاضی در علوم مختلف و به خصوص اقتصاد پرداخته و مثالهایی از قبیل Duopoly و انتخابات را بررسی میکنیم.
آشنایی با بیوانفورماتیک
توسط آقای احسان حق شناس
پنجشنبه 28 فروردین 1393، ساعت 17:30
چکیده :
بیوانفورماتیک یا به عبارتی زیستشناسی محاسباتی، یک زمینه بین رشتهای است که روشهای ذخیره سازی، بازیابی، سازماندهی و تجزیه و تحلیل دادههای زیستی را بررسی میکند. هدف اصلی بیوانفورماتیک درک بهتر و بیشتر فرآیندهای زیستی، نه از طریق روشهای آزمایشگاهی که از طریق طراحی الگوریتمها، بکارگیری تکنیکهای محاسباتی و توسعه نرم افزارها بر اساس آن الگوریتمها و تکنیکهاست. استفاده از مدلهای ریاضی و روشهای آماری برای حل مسائل نیز امری بسیار معمول در بیوانفورماتیک است.
در این سمینار ابتدا به معرفی این زمینه نسبتا جدید که به سرعت در حال رشد است میپردازیم. سپس جهت آشنایی بیشتر، مسئله de novo genome assembly را به عنوان نمونهای از مسائل موجود در این زمینه تحقیقاتی بررسی خواهیم کرد.
کدبرداری لیستی برای کدهای جبری
پنجشنبه 1اسفند 1392ساعت 17.30
توسط جناب آقای دکتر فرزاد پرورش، عضو هیئت علمی گروه برق دانشگاه اصفهان
چکیده : در این سخنرانی به معرفی کدهای رید-سلمون (RS) میپردازیم و سپس روشهای مختلف کدبرداری برای کدهای رید-سملون و کدهای مشابه آن معرفی میگردند. الگوریتمهای جبری موجود برای کدبرداری، عموماً زمانی قادر به کدبرداری خواهند بود که تعداد خطاهای موجود در کلمهٔ دریافتی کمتر از نصف کمترین فاصلهٔ کد باشد. در این حالت میتوان نشان داد تنها یک کدکلمه با کمترین فاصله از کلمهٔ دریافتی وجود دارد و الگوریتم کدبردار جواب یکتایی دارد. در حالتی که تعداد خطاهای کلمهٔ دریافتی از نصف کمترین فاصلهٔ کد بیشتر باشد، الگوریتم کدبردار لزوماً جواب یکتایی نخواهد داشت و الگوریتم باید قابلیت یافتن لیستی از کدکلمههای ممکن را به عنوان خروجی داشته باشد. ابتدا به الگوریتم سودان (Sudan) و گوروسوامی-سودان (Guruswami-Sudan) که قابلیت کدبرداری لیستی کدهای رید-سلمون را دارند زمانی که تعداد خطاهای کلمهٔ دریافتی از نصف کمترین فاصلهٔ کد بیشتر باشد و از باند جانسون (Johnson bound) کمتر باشد میپردازیم. سپس کدهای شبیه به کدهای رید-سلمون معرفی میگردند که دارای کدبردارهای جبری لیستی میباشند و قابلیت یافتن کدکلمههای ارسالی را دارند زمانی که تعداد خطاهای کلمه دریافتی کمی کمتر از کمترین فاصلهٔ کد باشد. چنین کدهایی با کدبردار لیستی معرفیشده قابلیت رسیدن به ظرفیت کانالهای گسسته با الفبای بالا را دارا میباشند.
مسئله پوشش در شبکههای حسگر تصویری
آقای احمد موحدیان عطار
دانشآموخته دانشگاه صنعتی اصفهان و پلیتکنیک لوزان
پنجشنبه 24 بهمن 1392، ساعت 17:30
خانه ریاضیات اصفهان
خوشهبندی دادهها بر اساس روشهای مبتنی بر گراف
سخنرانی، پنجشنبه 28 آذر1392، ساعت 16:30
دکتر رامین جوادی، استادیار دانشگاه صنعتی اصفهان
در این سمینار درباره کاربرد نظریه گراف در خوشهبندی دادهها، تقطیع تصویر و پردازش سیگنال گفتگو میکنیم. به ویژه خوشهبندی طیفی (خوشهبندی بر اساس طیف ماتریس تشابه) را به طور دقیق بررسی میکنیم.
مروری بر کدهای BCH و بررسی دو مسئله باز در کدهای RS (ریدسولومون)
پنجشنبه 17 بهمن 1392، ساعت 17:30
دکتر سعید مهرابی
کدهایی که در این سمینار مورد بررسی قرار میگیرند بر پایه میدانهای متناهی میباشد، لذا در ابتدا به معرفی ساختار و مفاهیم اولیه در میدانهای متناهی میپردازیم، سپس به بررسی کدهای دوری BCH که خود ر دو نوع (primitive BCH, non-primitive BCH) میباشند و در سال 1959 و 1960معرفی شدند خواهیم پرداخت. در ادامه به کدهای RS (ریدسولومون) که حالت خاصی از کدهای BCH و کدهای کدهای سمبلیک هستندمیپردازیم، این نوع کدها به علت عدم پیشرفت تکنولوژی در ابتدای معرفی در سال 1960 فقط از جنبه تئوری مورد توجه قرار گرفتند ولی امروز این نوع کدها کاربرد فراوانی در علوم ارتباطات دارند. در پایان به دو مسئله چالشی (open problem) در مورد کدهای RS خواهیم پرداخت.
سخنرانی داینامیکهای هم تکاملی
دکتر بهروز طوری
25 آبان 1392، ساعت 17:30
Coevolutionary Dynamics
چکیده: در سالهای اخیر مطالعه داینامیکها روی شبکهها (Dynamics on Networks) و همچنین چگونگی شکلگیری شبکهها (Networks Formation) مورد توجه فراوان محقفین قرار گرفته است که دلیل اصلی آن رونق چشمگیر شبکههای کامپیوتری و شبکههای اجتماعی و کاربردها و اثرات آنها در زندگی روزمره میباشد. اما با این حال تحقیفات پبرامون این دو موضوع به صورت مجزا صورت گرفته است و تحقیقات چندانی پیرامون داینامیکهایی که تاثیراتی روی شکل شبکه و شکل شبکه تاثیر در تغییرات آنها دارد، صورت نگرفته است. در این سمینار ما به معرفی کلی این چنین داینامیکها می پردازیم و یک مثال خاص از این داینامیکها، که معروف به مدل هگسلم- کراس برای مدل کردن شکلگیری نظر افراد در یک جامعه هست، را مورد بررسی عمیقتر قرار میدهیم.
بهروز طوری، دانش آموخته لیسانس مهندسی برق در دانشگاه صنعتی اصفهان، فوق لیسانس مهندسی برق دانشگاه ژاکوب برمن، آلمان و دکتری مهندسی صنایع دانشگاه ایلینوی اوربانا-شمپین بوده و هم اکنون محقق پسا دکتری در دانشکده مهندسی برق و کامپیوتر انستیتو تکنولوژی جورجیا است. زمینههای کلی تحقیقاتی مورد علاقه وی شامل تئوری کنترل و کنترل تصادفی، نظریه بازیها، و بهینه سازی است.
آیا آب دریا هم آشامیدنی ست ؟
اگر پدیده اُسمز را می شناسی، آری!
اعضای گروه ریاضیات در شیمی خانه ریاضیات
روز پنجشنبه 13/04/1392 ساعت 17:30
خلاصه سخنرانی :
بحران آب آشامیدنی یکی از معضلات بزرگ جهان امروزمی باشد. با توجه به اینکه بیشترین حجم آب های سطحی جهان را آب های شور تشکیل می دهد، بهترین راه برای حل این بحران استفاده از روشی است که بتوان آب های شور را شیرین نمود. روش اُسمز معکوس بهترین روش برای شیرین نمودن آبهای شور جهان می باشد. در این روش با محاسبه ریاضی دبی آب ورودی و خروجی و همچنین فشار مکانیکی اعمالی میتوان با بیشترین بازده آب دریا را شیرین نمود. برتری این روش بر سایر روشها به دلیل حذف کامل میکروارگانیسم ها و املاح موجود در آب میباشد.
به کارگیری یادگیری فعال در تجزیه وابستگی دستوری
سعید مجیدی
دانشجوی علوم کامپیوتر دانشگاه تافتس
12 بهمن 1392
برچسب گذاری مجموعههای نوشتاری ساختارمند (Structured Corpora)، ابزاری اساسی در تحقیقات نوظهور زبان شناسی است. با این حال جمعآوری این برچسبها هزینه بر میباشد. این وضعیت در مورد زبانهای تاریخی و یا زبانهایی که افراد کمی به صورت مادرزادی با آن تکلم میکنند بدتر است. برای تولید این برچسبها به صورت اتوماتیک، میتوان از تجزیه کنندههای وابستگی دستوری (Dependency Parser) استفاده نمود. اما تجزیهکنندههای دستوری دادهمحور، نیاز به مجموعههای نوشتاری برچسبگذاری شده بسیار بزرگ دارند تا بتوانند یادگیرند که چگونه درخت دستوری یک جمله را تولید نمایند. یادگیری فعال یک روش یادگیری ماشین است که در آن به یک سیستم در حال یادگیری اجازه داده میشود تا خود، دادههایی که برای یادگیری به آنها نیازمند است را انتخاب نماید. این دادهها معمولا دادههایی هستند که دارای بار اطلاعاتی بیشتری هستند. در این جلسه چارچوبی برای استفاده از یادگیری فعال جهت تجزیه وابستگی دستوری ارائه میشود.
” نتایجی جدید پیرامون قضیه های ناتمامیت گودل”
توسط جناب آقای دکتر پیام سراجی
پنجشنبه 30 خرداد 1392، ساعت 17:30
خلاصه سخنرانی:
در این جلسه بعد از مروری بر مقدمات قضیههای نا تمامیت، برخی نتایج جدید در زمینه این نظریه ها معرفی می شوند، از جمله اثبات جدیدی برای قضیه “گودل-راسر” و اثبات محاسبه ناپذیر بودن گزاره تصمیم ناپذیر در اثباتهایی كه “گ.چایتین” و “ج.بولوس” برای قضیه اول ناتمامیت ارائه دادهاند.
هندسه گرهها و ناورداهای آن
دكتر اكرم شیخ علیشاهی
5 اردیبهشت 1392
خلاصه سخنرانی :
گره ها به طور موثری با زندگی روزمره گره خورده اند! مثال های زیادی از گره ها را در معماری اقوام مختلف دیده و در زندگی روزمره و حرفه ای خود استفاده كرده ایم. اما مطالعه ریاضی گره ها بیش از یك قرن پیش با نظریه كلوین شروع شد. در تمام این سال ها همواره سوالات مهمی مانند اینكه چه موقع گرهی باز می شود؟! چگونه دو گره متفاوت را تمیز دهیم؟! مطرح بوده اند. در این سمینار به معرفی نظریه ریاضی گره ها و تعدادی از ناورداهای كلاسیكی كه به تشخیص گره ها كمك می كنند پرداخته و با سوالاتی آشنا می شویم كه به رقم صورت ساده، تا سالیان اخیر و معرفی ناورداهای (توپولوژیك) مدرن بدون پاسخ بوده اند!
بحثی پیرامون تلسكوپهای فضایی
فناوری مدرن ریاضیوار + ذهن کنجکاو انسان= تلسکوپ فضایی + درک والاتر از جهان
عمران مرادی
مدیر پروژه ساخت اولین تلسكوپ فضایی ایران
29 فروردین 1392
خلاصه سخنرانی :
ابعاد دنیای مدرن امروز آن قدر گسترده شده كه تا مرزهای جهان هستی پیشرفته است. روزگاری دانش نجوم به عنوان شاخه ای از ریاضیات سعی داشت با تكیه بر استحكام منطق ریاضی، نبود ابزار و فناوری لازم برای كشف و فهم جهان خلقت را جبران كند و این گونه بود كه از دل افسانه ها و بیان های شهودی درباره جهان هستی و اجرام فضا دانش ریاضی وار نجوم متولد شد. اگرچه ریاضیات توانست كمك های زیادی در جهت پیشرفت بشر در درك جهان هستی نماید اما همچنان جای ابزار و فن آوری خالی بود و ریاضیات هم دیگر نمی توانست این ضعف اطلاعاتی را جبران كند اما دنیای امروز دنیایی متفاوت است. امروزه فن آوری های پیشرفته بشری موجب شده است كه ناممكن های دیروز ممكن شود و بدون تردید می توان فن آوری های فضایی را در قله فن آوری مدرن امروزی دید.
در این میان تلسكوپ های فضایی، چشمان بشر خاكی شدند به فراسوی آن چه بشر قرن ها در فهم آن مانده بود تلسكوپ های فضایی كه زاییده ذهن شگرف و تكنولوژی بهت انگیز بشر امروزیست، دنیایی بسیار بسیار بزرگتر را برای بشر به ارمغان آوردند و موجب شدند مرزهای ذهن بشر نیز به همان اندازه بزرگ شود.
سمینار پیش رو بیان تصویری مختصر از ابهت این فن آوری پیچیده امروزی و تاثیر آن در درك انسان از جهان هستی است.
تنوع تلسكوپ های فضایی، و توجیه سرمایه گذاری در اینگونه پروژه های كلان مرتبط با فضا از محورهای دیگر مورد بحث در این سمینار خواهد بود.
بهینهسازی استوار
اعظم سلیمانیان
17 اسفند 1391
خلاصه سخنرانی :
در بسیاری از مسائل مهندسی، اقتصاد و مدیریت با مسائل بهینه سازی مواجه هستیم كه پارامترهای مسئله با نوعی عدم دقت (عدم دقت اندازه گیری و …) یا عدم قطعیت (نا مشخص بودن مقدار پارامتر برای برنامه ریزیهای آینده مانند قیمت سهام یا میزان تقاضا و …) درگیر هستند. حال اگر قرار باشد به ازای هر تغییر پارامتر مسئله از ابتدا با پارامترهای جدید حل شود به نوعی درگیر روش آزمون و خطا شدهایم كه دفعات حل مسئله یا تعداد آزمایشات لازم به صورت نجومی بالا میروند و به تبع آن هزینه و وقت بسیاری صرف این آزمایشها میشود. پس منطقا باید به دنبال روش حلی باشیم كه نسبت به این تغییرات پارامترها مصون باشد تا بدین ترتیب در وقت و هزینه صرفه جویی شود و جواب حاصله در طول زمان كارایی خود را از دست ندهد.
از طرف دیگر در بسیاری از مسائل واقعی با “قیدهای سخت” مواجه هستیم یعنی قیودی كه تحت هر شرایط و به ازای هر تغییر پیش بینی شدهای در پارامترها باید همچنان برقرار باشند. مانند “قیود كنش” كه مربوط به استحكام یك سازه (مانند پل یا بدنه هواپیما) هستند و یا قیود مربوط به مسائل سبد سهام و سایر سرمایه گذاریهای حساس كه نقض قید به ازای یكی از مقادیر عدم قطعیت ممكن است منجر به خسارت سنگین یا فروپاشی سازه شود. روش “بهینهسازی استوار” برای چنین مسائلی پیشبینی شده است و با توجه به اهمیت ویژه این مسائل نیاز به كار و تحقیق در حوزه بهینهسازی استوار به خوبی قابل درك است. از این رو در این سمینار به مبحث بهینهسازی ریاضی و بخصوص بهینه سازی استوار میپردازیم.
cognitive distribute system
استاد دانشكدههای برق و كامپیوتر و ریاضی و آمار
كانادا Queens University دانشگاه
7 دی 1391
خلاصه سخنرانی:
in this talk, we intuitively use the human cognitive system in order to give ideas and a roadmap for future technologies in a lay language. the goal of cognitive distributed statistical signal processing technologies is to monitor events and changes in distributed infrastructures such as wireless communications, power grids and radars. traditional network infrastructure incorporates little to no cognition. cognition-based systems can intelligently and dynamically alter and reconfigure themselves to enhance resource management . they can also learn from past situations, decisions and actions in order to improve future outcomes. advanced and low-cost algorithms are the key to next-generation technology. these infrastructures hold a significant place in the economy in terms of employment and revenue. the cognitive management of scarce distributed resources promises to enhance the efficiency of these critical infrastructures. as modern society increasingly relies on mobile connectivity, spectrum demand is increasing. this ever-increasing demand has led to re-evaluation of spectrum utilization and highlighted the necessity for cognitive thechnologies to gather and act on information about the medium and users to improve network efficiency, save energy, and lower costs. many problems to be solved arise when distributed elements must make a collective set of decisions and have limited ability to exchange information.
تکنیکهای داده کاوی در بازاریابی، فروش و مدیریت ارتباط با مشتری
مسعود فاتحی
9 آذر 1391
خلاصه سخنرانی: در این سمینار ابتدا خلاصهای از یت داده كاوی ارائه میشود. سپس به برخی از مفاهیم اساسی در مباحث فروش، بازاریابی مستقیم و مدیریت ارتباط با مشتری اشاره شده و كاربرد تعدادی از تكنیك های داده كاوی در این زمینهها با ذكر مثالهایی توضیح داده میشود.
جایگاه هندسه تناسبات در معماری ایرانی با نگاهی به پیمون
4 آبان 1391
علی محمد رنجبر كرمانی
خانه ریاضیات اصفهان، بخش ریاضیات و هنر، سخنرانی ویژه ای در گستره ی پیوند دانش ریاضیات و هنر برگزار می كند.
خلاصه سخنرانی: در معماری ایرانی همواره روابط مشخصی بین اندازههای بكار رفته در فضاهای معماری موجود میباشد. برخی این نسبتها در بناها بیشتر رخ مینمایند. این سخنرانی بر آن است تا پس از بررسی كوتاهی درباره ی كاربرد دانش هندسه در معماری، به بررسی این اندازهها پرداخته و نمونههای موردی آن را در گذر زمان پیگیری كند.
قانون جمع سرعتهای نسبی انیشتین و هندسه هذلولوی
فاطمه شیخ بهائی
20 مهر 1391
خلاصه سخنرانی: دراین سمینار براساس كارهای دو ریاضیدان برجستهی معاصر ، پرفسور هلموت كارتسل وپرفسور آبراهام اونگار با روشی نو چشم اندازهای جدیدی از هندسه هذلولوی به كمك جایروفضای برداری گشوده میشود . این رهیافت شباهتهای عمیقی با رهیافت معمولی فضای برداری در هندسه ی اقلیدسی دارد . این شباهت ها به ما امكان میدهد كه دانش مربوط به هندسهی اقلیدسی وفیزیك كلاسیك نیوتنی وابسته به آن را به شكل شهودی به هندسهی هذلولوی وفیزیك نسبیتی مربوط كنیم.
كمی هندسه و توپولوژی با طعم كیهان شناسی
مهدی شریف زاده
31 مرداد 1391
خلاصه سخنرانی: در این گفتمان به بررسی چند نوع توپولوژی خاص روی یك فضا زمان می پردازیم كه این توپولوژی ها به كمك یك رابطه ترتیب روی فضازمان تعریف می شود. از آنجا كه در تعریف این رابطه ترتیب از مفاهیم علیتی﴿ causality ﴾ استفاده می شود ابتدا به معرفی یك فضا زمان و روابط علی موجود در آن ﴿ البته به ساده ترین شیوه ای كه ارائه دهنده می داند ﴾ می پردازیم.
معرفی سیستم رمزی دوگان RSA و بررسی آن
سمیه مرادی
20 تیر 1391
خلاصه سخنرانی:
در این سمینار ما به معرفی یك سیستم جدید به نام دوگان RSA می پردازیم كه از دو نمونه متفاوت RSA با ن ای عمومی و خصوصی یكسان و پیمانه های متفاوت تشكیل شده است . این سیستم به دلیل داشتن ن ای عمومی و خصوصی یكسان، حافظه مورد نیاز برای ذخیره كلیدها را كاهش میدهد كه در نتیجه برتری این سیستم را در زمانی كه نیاز به استفاده از دو سیستم RSA باشد نسبت به سیستم هایی مانند RSA* ۲ و دو قلوی RSA میرساند.
نانو تكنولوژی و مدلسازی
ساناز خادم القرآنی
22 تیر 1391
خلاصه سخنرانی: امروزه نانوتكنولوژی از مباحث مطرح در شاخههای متعددی از علوم مثل رسانش دارو، تغذیه، الكترونیك ، منابع شیمیایی و غیره است . موضوع اصلی نانوتكنولوژی مهار ماده یا دستگاه های در ابعاد كمتر از یك میكرومتر، معمولا حدود ۱ تا ۱۰۰ نانومتر است. در واقع نانوتكنولوژی فهم و به كارگیری خواص جدیدی از مواد و سیستمها در این ابعاد است . به طور كلی فناوری نانو به سه سطح قابل تقسیم است: مواد، ابزارها و سیستمها. موادی كه در سطوح نانومتری این فناوری به كار میرود را نانو مواد مگویند. به هر مادهای كه حداقل یكی از ابعاد آن در مقیاس زیر ۱۰۰ نانومتر باشد، یك نانوماده اطلاق میشود. در این رابطه اندازه مواد بر عملكرد آنها تاثیرگذار میباشد. از جمله مواد مطرح در بخش نانوتكنولوژی ، نانوذرات است. الكترواسپری یكی از جدیدترین روشهای تولید نانوذرات است . در این فرصت، ضمن نگاهی بر نانوتكنولوژی ، به روشهای تولید نانومواد اشاره نموده و به تغییرات خواص مواد بر اثر تغییر اندازه میپردازیم . سپس با توجه به اهمیت اندازه ذرات، با اشاره ای بر مدل سازی، مدلی را برای اندازه نانو ذرات تولید شده به روش الكترو اسپری جهت پلیمر ارائه میدهیم.
بهینه سازی سبد سهام
زِینب سجادیه
11 خرداد 1391
خلاصه سخنرانی: الگوریتمهای تكاملی ، تكنیكهای بهینه سازی تصادفی هستند كه بر روی یك جمعیت یا مجموعهای از جوابها كار می كنند و در نهایت با توجه به تابع برارزش وهمچنین عملیات مختص مربوط به نوع الگوریتم، به جواب بهینه دست پیدا میكنند .یكی از معروفترین این اگوریتمها، الگوریتم ژنتیك و یكی از جدیدترین آنها الگوریتم رقابت استعماری است. در پژوهش انجام شده هر دو الگوریتم مذكور برای حل یك مدل بهینه سازی سبد سهام به كار گرفته شدهاند .از آن جایی كه هدف از یك سرمایه گذاری داشتن حداكثر بازدهی و حداقل ریسك است لذا یك مدل بهینهسازی، با هدف بیشینه كردن سود و براساس ریسكی معین به كار گرفته شده است. معیار ریسك استفاده شده در این مدل، ارزش در معرض خطر است. این معیار یكی از شاخصهای مهم اندازهگیری ریسك بازار است. پس از پیادهسازی الگوریتم رقابت استعماری و مقایسه آن با الگوریتم ژنتیك برای این مسئله، نتایج نشان از برتری قابل توجه الگوریتم رقابت استعماری دارند، به این معنا كه الگوریتم رقابت استعماری علاوه بر آن كه سود بیشتری را به دست میآورد، زمان كمتری را نیز برای رسیدن به آن صرف میكند.
از شیمی بیاموزیم اكسیر كردن بدیها و احیا كردن خوبیها
تیم تحقیقاتی شیمی
14 اردیبهشت 1391
خلاصه سخنرانی : بیشتر پدیده های طبیعی مثل گیاهان ، حشرات وحیوانات دارای درجهای از تقارن هستند وعموم مردم حداقل یك برداشت كیفی از تقارن دارند. به تصویری از یك گل زیبا ، یك پروانه یا ساختمان آزادی واهرام ثلاثه مصر نگاه كنید ، بخشی از شكوه وزیبایی این پدیدههای طبیعی ، آثار هنری و معماری، ناشی از تقارن به كاررفته درآن هاست. جاودانگی وجذابیت شعر و ادب فارسی نیز تحت تاثیر نظم و یا به عبارتی تقارن آن است. در مقیاس مولكولی نیز درجاتی از تقارن وجود دارد كه شناخت و استفاده از آن در علم شیمی، در شناخت ومطالعه مولكولها بسیار مفید است.
سخنرانی تحت عنوان “محدودیتهای علم ریاضی”
مسعود صدیقین
پنجشنبه 31 فروردین – ساعت 17:30
خانه ریاضیات اصفهان
خلاصه سخنرانی: قدرت ریاضیات تا چه حد است ؟ توان رایانه در حل مسائل چقدر میباشد ؟ شاید پاسخهای افرادی چون گودل ونورینگ به این سوالها تا اندازه ای قادر به نشان دادن محدودیت این علوم باش . آیا مجموعه اعداد حقیقی شمارش پذیر میباشند ؟ در نگاه اول پاسخ این سوال به سوالات بالا نامربوط به نظر میرسد. اما روش كارنتور در اثبات شمارش ناپذیری اعداد حقیقی در پاسخ به گوشهای از سوالات بالا كمك كرد. او از روشی بسیار ساده به نام قطری سازی استفاده كرد. این روش به سرعت مورد استفاده سایر ریاضی دانان برای اثبات مسائل دیگر شد. یت پارادوكس گونه روش معمولا برای اثبات عدم وجود یك خاصیت مورد استفاده قرار میگیرد. از جمله مسالههایی كه از این روش استفاده میكنند مساله توقف میباشد. چارچ تورینگ نشان داد هیچ الگوریتمی برای تشخیص اینكه آیا یك برنامه بر روی یك ورودی متوقف میشود یا خیر وجود ندارد. با گسترش این مساله نمونههایی از مسائل حل نشدنی در زمینههایی مانند كاشی كاری و نظریه اعداد معرفی شد . قضیه ناكاملی گودل نیز كه بر مبنای همین روش میباشد از قضایای اساسی در مورد تواناییها و محدودیتهای علم ریاضیات میباشد. در این جلسه هدف معرفی روش قطری سازی واستفاده آن در حل مسائل مطرح شده بالا و همچنین معرفی مسالههای تصمیم نا پذیر در علم ریاضیات میباشد.
چگونه با یک مجموعه کد بسازیم
سمیه سماعی
17 فروردین 1391
خلاصه سخنرانی : یك مجموعه تفاضی زیر مجموعهای از مجموعه اصلی است كه میتوان با تفاضلات اعضای آن، كل مجموعه اصلی را تولید كرد. با پیدایش علم كدگذاری، انواع مجموعههای تفاضلی با توجه به كاربرد آنها در نظریه كدگذاری، بسیار مورد توجه محققان قرار گرفتند به طوری كه این مسئله گروهی از پژوهشگران را بر آن داشت تا گروههای متناهی را بر مبنای وجود یا عدم وجود مجموعههای تفاضلی در آنها رده بندی كنند. در این سمینار روند تولید كد از یك مجموعه تفاضلی و شرایط وجود كدهای باینری بر این مجموعهها را بررسی می كنیم . در این راستا با استفاده از تفریف طرح و ماتریس هادامارد به تعریف كد بر این مجموعهها خواهیم پرداخت. در آخر با تعمیم مجموعههای تفاضلی بر گروهها، به بررسی وجود یا عدم وجود كد بر تعدادی از گروهها خواهیم پرداخت .
مدلسازی و بهینهسازی سیستمهای مكاترونیك و رباتیك
مهرناز آقانوری – علی اسماعیلی
4 اسفند 1390
خلاصه سخنرانی: سیستم مكاترونیكی به سیستمی گفته میشود كه از مجموعه سیستمهای مكانیكی، الكتریكی و كامپیوتری تشكیل شده باشد. با توجه به گسترش روزافزون سیستمهای مكاترونیكی در جهان امروز، مدل سازی و بررسی این سیستمها و به دست آوردن معادلات دینامیكی آنها امری مهم و چالش برانگیز است. همچنین بهینه سازی پارامترهای آنها مساله مهمی است كه شیوه مدل كردن، عامل موثری در دستیابی به این هدف محسوب میشود. از آنجا كه رباتها از مهمترین سیستمهای مكاترونیكی به شمار میروند، در این سمینار مدل سازی و بهینه سازی این سیستمها مورد بررسی قرار میگیرد.
فرایندهای لوی در ریاضیات مالی
صابر مهدی زاده
13 بهمن 1390
خلاصه سخنرانی: نظریه فرآیندهای تصادفی یكی از مهمترین پیشرفتهای علمی است. از دیدگاه شهودی هدف این نظریه الگوسازی شانس به كمك زمان است. رده خاصی از فرآیندهای تصادفی موسوم به فرآیندهای لوی هستند. ساختار اساسی این فرایند در دوران طلایی نظریه احتمال در دهه ۱۹۴۰ – ۱۹۳۰ توسط لوی، ریاضیدان روسی خینچین و ایتو در ژاپن شناسایی گردید. در سالهای اخیر به دلیل پیشرفتهای نظری و همچنین گستره وسیعی از كاربردهای جدید به ویژه در ارزیابی قراردادهای اختیار معامله در مدیریت مالی علاقه به این فرآیند افزایش یافته است.
اثبات قضیه آخر فرما
علی رجالی
29 دی 1390
خلاصه سخنرانی : قضیه آخر فرما به عنوان یك سوال مقدماتی كه ۳۵۰ سال ریاضیدانان را به خود مشغول داشته بود و ركورددار بیشترین حل غلط ارائه شده بود حائز اهمیت نیست، بلكه چنانچه توضیح خواهیم داد تلاشهای نافرجام برای اثبات آن سبب ایجاد شاخههای مهمی چون جبر جابجایی و هندسه جبری حسابی گردید و شگفتا كه حل نهایی آن هم افقهای جدیدی در نظریه اعداد، هندسه جبری، نظریه نمایش و بسیاری شاخههای دیگر برای ما گشوده است.
مربعهای جادویی
رسول سلیمی
1 دی 1390
خلاصه سخنرانی: مربع جادویی یا وفقی جدولی است دارای n*n خانه كه خانه های آن با عددهای مثبت از ۱ تا n به ترتیبی پر شده است كه مجموع عددهای هر ردیف افقی و یا هر ستون عمودی و یا هر قطر آن، عددی ثابت را نشان میدهد. در این سمینار به بررسی موارد زیر پرداخته میشود :
– معرفی روش خاص برای پركردن مربعهای جادویی زوج به كمك روش هستهای -پوستهای با مرتبه دلخواه ﴿ قابل افزایش به هر مرتبه ۲۰*۲۰، ۲۲*۲۲، ۲۴*۲۴و … ﴾
– فرمول عمومی همه مربعهای جادویی با مرتبه زوج و مرتبه فرد بهطوریكه به ازای همه مقادیر وفق برقرار باشد .
– پر كردن مربعهای ۳*۳ با اعداد اول به طوریكه وفق بر قرار باشد .
– پیشنهاد و بررسی استفاده از مربعهای جادویی در رمزنگاری با توجه به داشتن فرم عمومی آن
مهندسی خلاقیت (TRIZ)
محمد الهیاری
3 آذر 1390
خلاصه سخنرانی: سمینار را با ذكر تاریخچهای از پیدایش تفكر خلاق شروع كرده و در باب موضوعات بالا بحث میكنیم سپس به بیان TRIZ پرداخته و ….
كاشیكاری در آموزش ریاضی
مقداد قاری
7 دی 1390
خلاصه سخنرانی : كاشیكاری یكی از شاخههای هندسه است كه بسیار ساده و قابل فهم برای دانشآموزان همه مقاطع بوده، وسیلهای جذاب برای آموزش بسیاری از مفاهیم ریاضی است. در این سخنرانی به بررسی چند كاربرد از كاشیكاری در آموزش ریاضی میپردازیم و كارگاه زیر را برای این منظور پیشنهاد می دهیم: كاشیكاری با چند ضلعی های محدب، كاشیكاریهای منتظم و ارشمیدسی، كاشیكاریهای اشر و تبدیلات هندسی، گروه های تقارن كاشیكاریها، كاشیكاریهای اسلامی
zero-stability of a multistep method
شایسته ممهد
24 شهریور 1390
خلاصه سخنرانی : مطالعه بر روی پایداری و رفتار مجانبی برخی از سیستمهای دینامیكی گسسته موضوع مهمی در بسیاری از شاخههای ریاضیات و مهندسی است. ایده این سمینار برای من از این سوال شروع شد: چه عامل یا عواملی در یك معادله دیفرانسیل بر پایداری آن تاثیر میگذارد؟ در این سمینار ما سعی میكنیم با ارائه روشی برای گسسته سازی ODEها و پیاده كردن روشهایی برای حل عددی این معادلات به دنبال دامنه مناسبی از نسبت اندازه گامها بگردیم كه در آن معادله پایدار است .
ریاضیات تصادفی
مریم وحید
3 شهریور 1390
خلاصه سخنرانی : ریاضیات تصادفی شاخهای جوان و هیجان انگیز از ریاضیات است كه به جای متغیرهای وتوابعی تعینی با متغییرهای تصادفی و توابعی از آنها سر وكار دارد، واز این طریق پای احتمال و فرایند تصادفی را به حوزههای مختلف ریاضیات باز میكند. تركیب این دو ابزار قدرتمند مدل سازی و تحلیل بسیاری از مسائل را به گونهای سادهتر امكان پذیر میسازد.در این سخنرانی باب آشنایی با این مبحث در ریاضیات را باز كردهایم.
چگونگی تركیب محرك های مختلف توسط مغز
مسیح رحمتی
9 مرداد 1390
خلاصه سخنرانی : مغز انسان یكی از پیچیدهترین و شگفت انگیز ترین سیستمهای موجود در طبیعت است كه مجموعهای از فعالیتها در سطوح مختلف را در شرایط گوناگون انجام میدهد. عملكرد كلی مغز به این صورت است كه محركهای بیرونی را دریافت و پردازش كرده و سپس واكنش لازم را انجام میدهد. فرایندهای پردازش، تصمیمگیری و واكنش دارای مدلهای ریاضی بسیار پیچیده بوده كه مغز بسیاری از آنها را به صورت بهینه انجام میدهد. در این سمینار به بررسی عملكرد مغز در فرایند تركیب محركهای مختلف ﴿ برای مثال صدا و تصویر ﴾ به ویژه مدل ریاضی آنها و همچنین پیاده سازی این مدل توسط شبكههای عصبی میپردازیم .
رنگ آمیزی ستارهای گرافها
الهام روشن بین
30 تیر 1390
خلاصه سخنرانی :
رنگ آمیزی گرافها یكی از مباحث اصلی نظریه گراف است. ساده ترین نوع رنگ آمیزی كه در واقع نقطه شروع این مبحث است، رنگ آمیزی معتبر راسی است، یعنی یك تخصیص از رنگها به راسهای یك گراف به طوری كه هیچ دو راس مجاوری هم رنگ نباشند. در كنار انواع كلاسیك و تعمیمهای مختلف رنگ آمیزی گرافها، با گذاشتن محدودیت روی روش تخصیص رنگها میتوان به حالتهای گوناگونی از رنگ آمیزی دست یافت. از جمله این حالتهای خاص رنگ آمیزی ستارهای است. در این سمینار ضمن آشنایی بیشتر با این نوع رنگ آمیزی، برخی ازنتایج به دست آمده پیرامون رنگ آمیزی ستارهای گراف ها را نیز مشاهده خواهیم كرد.
مجموعه مستقل بیشینه گرافها”
روز پنجشنبه 6 خرداد سال 89 ساعت 17:00
توسط جناب خانم پریسا مزروعی
سخنرانی: نظریه گرافها شاخهای از ترکیبیات است که در مدل کردن بسیاری از مسائل پیچیده توانا بوده و به صورت گستردهای مورد استفاده قرار میگیرد. از جمله این مسائل میتوان به پیدا کردن بزرگترین مجموعه مستقل خطی در یک گراف اشاره کرد که کاربردهای فراوانی در تئوری اطلاعات و بیولوژی ملکولی molecular biology دارد. این مسئله و مسائل معادل با آن از دسته مسائل hard-NP هستند و تاکنون هیچ الگوریتم محاسبه پذیری (در زمان قابل قبول) برای آنها یافت نشده است. در این سمینار قصد داریم به بررسی دقیقتر این مسئله بپردازیم.سپس رویکردهای مختلف حل این مسئله را بررسی و راه حل محاسبه پذیری برای این مسئله در کلاس خاصی از گراف ها ارائه کنیم.
ملاحظاتی پیرامون منطق فازی
آقای پیام سراجی
روز پنج شنبه23/8/87 ساعت 17:00
خلاصه سخنرانی: در این جلسه ابتدا به مبانی فلسفی علم منطق (به معنای کلی) و رابطه “زبان” با “معنا” میپردازیم و سپس به مبانی منطق کلاسیک و منطق فازی پرداخته و مقایسهای بین این دو انجام میدهیم. در پایان سعی میکنیم جایگاه هر یک از این منطقها را در مبانی ریاضی، مسائل فلسفی و مسائل کاربردی مشخص کنیم.
مکان، زمان، کیهان
احسان رعنایی
تاریخ سمینار: 3/8/1386
خلاصه سمینار: مسلما همه ما پیرامون ابعاد بالاتر مانند بعد چهارم شنیدهایم. این سمینار مطلب جدید و مهمی در بر ندارد و بیشتر سعی به تشریح دیدگاهی از این بعد که مبنی بر توصیف ساختار کیهان در نظریه نسبیت شده، دارد. در این سمینار با کمترین استفاده از فرمول تلاشی فکری برای تحلیل شماتیک ساختار جهان اطراف از منظر یک بعد بالاتر داریم، هرچند منجر به نتیجهگیری خاصی نشود.
مکان، زمان، کیهان 2
خلاصه سمینار: در سمینار قبلی، توضیحات کلی و پراکندهای پیرامون دیدگاههای هندسی بعد چهارم ارائه شد. در سمینار دوم ضمن مرور مباحث مذکور برای افرادی که در جلسه اول حضور نداشتهاند، مقدماتی پیرامون ارتباط این دیدگاهها با نظریه نسبیت و کیهانشناسی که مربوط به ساختار کلی جهان است مورد بررسی قرار میگیرد. از شرکتکنندگان انتظار میرود بدون توجه به سطح اطلاعات خود در این زمینه، به نقد و تحلیل دیدگاهها بخصوص موارد مربوط به کلیات هندسی و شماتیکی پردازند، هر چند منجر به نتیجهگیری خاصی نشود.
مکان، زمان، کیهان 3
خلاصه سمینار: ابتدا به مرور مطالب 2 سمینار قبل برای افرادی که در آن جلسات حاضر نبودهاند، میپردازیم. ارزش این سمینار، تنها تلاش فکری و تحلیلی شرکت کنندگان ( بدون توجه به سطح اطلاعات و رشته پژوهشی) بهمنظور تصور و مدلسازی هندسی کیهان از منظری فرا مادی به گونهایست که با مشاهدات ه نگ نماید، هرچند منجر به نتیجهگیری خاصی نشود. لذا برخی خواص ملموس کیهان مرور و بررسی و به برخی اندیشهها مانند نظریه نسبیت اشاره خواهد شد.
سینمای ریاضی
ارائه دهنده: بهروز طوری
تاریخ سمینار: 1/6/1386
خلاصه سمینار: میخواهیم در این سمینار با دیدگاه ریاضی به فیلم سینمایی نگاه کنیم و ببینیم که چه سوالات ریاضی چالش برانگیزی در این راستا وجود دارد. سپس خواهیم دید که چگونه با پاسخ به این سوالات در سینمای ریاضی میتوانیم مسائلی از جمله قضیه اصلی حسابان (که هر چندجملهای درجه n دارای n ریشه متمایز است) را حل کنیم (البته درصورت وجود وقت کافی). به نظر شما چگونه این کار امکانپذیر است؟
روی آوردن یا نوآوردن
ارائه دهنده: محمد الهیاری
تاریخ سمینار: 18/5/1386
خلاصه سمینار:
Brun’s Sieve method is perhaps our most powerful elementary tool in N.theory “P.Erdos”s
ازBrun میگوییم و نوآوریاش
ازSelberg میگوییم و تیزبینیاش
بهLinik میرسیم وآینده نگریاش
ازRenyi میگذریم با دستاورد مهماش
بهChen میرسیم و جرات هجوم به ناشناختهها و…
و حالا به دنبال کسی میگردیم که این کار ناتمام را به اتمام برساند.
ریاضیات و نجوم
ارائه دهنده: آقای زمانی
تاریخ سمینار: 11/5/1386
خلاصه سمینار: در این سمینار تاثیرپذیری متقابل نجوم و ریاضی بررسی میشود. نجوم رشتهای است که ریاضیات زبان آن است.گالیله میگوید: “فیزیک و نجوم هم کتاب خدا هستند اما به زبان ریاضی”.
بسیاری از کشفیات و فرضهای فیزیکی و ریاضی ارائه شده، در اثر نیازهائی که علم نجوم به آنها داشته، بهوجود آمدهاند. پیشرفتهای جدید علم نجوم مدیون پیشرفتهای ریاضیات و محاسبه رصدهای دقیق کامپیوتری است.
پیرامون بعد هاسدورف
4 مرداد 1386
شفیع شکرانی
گرچه حدود یک قرن است که بُعد هاسدورف کشف شده، ولی میتوان گفت در دو، سه دهه اخیر است که کارهای اساسی روی این بُعد شکل گرفته و قبل از آن شاید بخاطر خواص پیچیدهای که دارد آنچنان مورد توجه قرار نگرفته است. از مهمترین دلایل مورد توجه قرار گرفتن این بُعد، میتوان بررسی سیستمهای دینامیکی (مختلط ) پیچیده را نام برد که با پیشرفت علوم کامپیوتر جدیتر شده است.
بُعد هاسدورف نیز، به عنوان یکی از مشخصات این مجموعههای تازه روی کار آمده، خواص جالب و پارادوکس گونهای از خود نشان میدهد.
یادگیری تقویتی (Reinforcement Learning)
سعید مجیدی
21 تیر 1386
یادگیری تحت سرپرستی، یک روش عمومی در یادگیری ماشین است که در آن به یک سیستم، مجموعه جفتهای ورودی – خروجی ارائه شده و سیستم تلاش میکند تا تابعی از ورودی به خروجی را فرا گیرد. یادگیری تحت سرپرستی نیازمند تعدادی داده ورودی به منظور آموزش سیستم است. با این حال ردهای از مسائل وجود دارند که خروجی مناسب که یک سیستم یادگیری تحت سرپرستی نیازمند آن است، برای آنها موجود نیست. این نوع از مسائل چندان قابل جوابگویی با استفاده از یادگیری تحت سرپرستی نیستند. یادگیری تقویتی مدلی برای مسائلی از این قبیل فراهم میآورد.در یادگیری تقویتی(Reinforcement Learning)، سیستم تلاش میکند تا تقابلات خود با یک محیط پویا را از طریق خطا و آزمایش بهینه نماید. یادگیری تقویتی مسئلهای است که یک عامل که میبایست رفتار خود را از طریق تعاملات آزمایش و خطا با یک محیط پویا فرا گیرد، با آن مواجه است. در یادگیری تقویتی هیچ نوع زوج ورودی- خروجی ارائه نمیشود. به جای آن، پس از اتخاذ یك عمل، حالت بعدی و پاداش بلافصل به عامل ارائه میشود. هدف اولیه برنامهریزی عاملها با استفاده از تنبیه و تشویق است بدون آنکه ذکری از چگونگی انجام وظیفه آنها شود. در این سمینار ابتدا مسئله یادگیری تقویتی معرفی شده و سپس الگوریتمهای مختلف مطرح در آن بیان میشوند.
تکامل استراتژی ه نگ سازی بوسیله برنامه نویسی ژنتیک شبکهای
آرمین توکلی
15 تیر 1386
یجاد ه نگی میان عاملهای موجود در یک سیستم چندعاملی، یکی از مهمترین مسائل در اینگونه سیستمها میباشد. یافتن، طراحی و پیاده سازی استراتژی ه نگ سازی اگر نگوییم غیر ممکن، بسیار دشوار است. امروزه زمینه یادگیری ماشین چند عاملی، نوید راهکارهای جدیدی برای حل مسئلهی ه نگسازی عاملها، در سیستمهای چند عاملی را میدهد.
در این سمینار، برنامهنویسی ژنتیک شبکهای برای ایجاد ه نگی میان عاملهای صیاد در دامنه تعقیب (صیاد-صید) به کار گرفته شده و میزان تاثیر و موفقیت آن بررسی میشود.
Face Recognition
نسیم شمس
20 اردیبهشت 1386
تشخیص چهره یکی از زمینههای تحقیقاتی است که در سالهای اخیر بسیار مورد توجه قرار گرفته. به طور کلی هدف اصلی در این کار تشخیص هویت یک فرد از روی یک تصویر ثابت و با استفاده از اطلاعات موجود در یک data base است. تغییرات نور محیط, تغییر جهت و حالت صورت از جمله موانع تشخیص چهره به شمار میآیند. تشخیص چهره را میتوان یک مساله تشخیص الگو با ابعاد بالا در نظر گرفت. اما در اصل ابعاد و مولفههای صورت بسیار کمتر از ابعاد صورت در تصویر خام است.این مساله نقطه شروع استفاده از روشهای آماری و زیر فضاهایی مانند PCA(Principal Component Analysis) و ICA (Independent Component Analysis) است که در میان الگوریتمهای تشخیص چهره بسیار موفق هستند و به خاطر قابلیت کاهش ابعاد و سادگی پیاده سازی مورد توجه میباشند. صحت نتایج بدست آمده از این روشها تا حد زیادی بستگی به این امر دارد که ویژگیهای صورت با چه دقتی از تصویرهای نمونه استخراج شوند. بنابرین میتوان با اجرای تکنیکهای feature extraction قبل از PCA و ICA درصد تشخیص صحیح را بالا برد. تبدیل موجک یکی از تبدیلهایی است که برای feature extraction استفاده میشود. در این روش ابتدا صورت توسط تبدیل موجک به فرکانسهای مختلف تجزیه و برای انجام عملیات در زیر فضاها آماده میشود.
Singular Value Decomposition in Pattern Recognition
مسیح رحتمی
در دهههای اخیرeigen decomposition در الگوریتمهای زیادی در زمینههای متفاوت مهندسی مورد استفاده قرار گرفته است.بردارهای ویژه و مقادیر ویژه در کل مفاهیم بسیار مفیدی به حساب میآیند، ولی محدودیت آنها به ماتریسهای مربعی استفادههای آنها را در بسیاری مسائل با مشکل مواجه مینماید. تجزیه دیگری از یک ماتریس وجود دارد به نام singular value decomposition (SVD) که میتواند این مشکل را برطرف نماید. SVD گسترهی وسیعی از کاربردها ،از digital signal processing، بیوانفورماتیک و مهندسی پزشکی، بهینه سازی وکنترل تا جغرافیا را در بر میگیرد.
به طور خلاصه هر ماتریس حقیقی مستطیلی میتواند به فرم حاصل ضرب 3 ماتریس بخصوص نوشته شود. این ماتریسها قابلیتهای مفیدی در اختیار ما میگذارند. ما میتوانیم اطلاعات مفیدی از هر یک از این 3 ماتریس استخراج کنیم. در این سمینار قصد داریم این تکنیک و برخی از ویژگیها و کاربردهای آن را معرفی نماییم.
Decision Making
امیر محمد نادری
17 اسفند 1385
با توجه به این که در تمامی موارد زندگی، انسان تصمیمگیریهای لازم را انجام میدهد، تصمیمگیری امری مهم تلقی میشود. ما در مواردی مانند خرید ماشین، انتخاب رنگ لباس، تست زدن در امتحان و… از فرآیند تصمیمگیری استفاده میکنیم.
در این سمینار به بررسی و مدلسازی فرآیند تصمیمگیری با استفاده از ابزارهائی مانند منطق فازی، شبکههای عصبی و الگوریتمهای ژنتیک میپردازیم.
نظریه گروهها
مازیار سنجابی
26 بهمن 1385
گروه مفهوم مجردی است که در ریاضیات سابقهای بسیار طولانی دارد.امروزه نظریه گروهها بخش بسیار وسیعی از ریاضیات و به خصوص جبر را دربرگرفته است.
این مفهوم به واسطه سادگی تعریف و برخی از خواص آن که وام گرفته از برخی مجموعههای متداول ریاضی است و همچنین کاربرد به نسبت وسیعش همواره مورد علاقه پژوهشگران و ریاضیدانان بوده است.گرچه بحث کوتاهی در این زمینه به هیچ وجه نمیتواند حق مطلب را ادا کند، ولی ما در این نشست سعی میکنیم تا جائی که میتوانیم این مبحث را گسترش دهیم. یکی از جنبههای جذاب نظریه گروهها این است که خواندن آن نیازبه هیچ گونه پیش نیازی ندارد و این بخش از ریاضیات تا حدود زیادی وابسته به شاخههای دیگر ریاضی نیست و خواندن آن تنها یک قلم، یک کاغذ و یک کتاب خوب میخواهد.
فضای حالت
بهروز طوری
21 دی 1385
Psyco Acoustic
دکتر سعید گازر
2 دی 1385
در این سخنرانی ضمن اشاره به اصول شنوائی، ارتباط علوم ریاضی و روانشناسی را با آن بررسی و سپس به برخی از کاربردهای آن در زمینه کمک به ناشنوایان و همچنین کاربردهایی در صنعت پرداخته میشود.
تئوری ریاضی موسیقی
جلسه اول : 30 شهریور 1385
جلسه دوم : 6 مهر 1385
پیام سراجی
از زمان فیثاغورث موسیقی و ریاضی ارتباط نزدیکی با هم داشتهاند و موسیقی در کنار حساب، هندسه و نجوم از چهار مبحث اصلی ریاضی محسوب میشده است. در این جلسه، تئوری موسیقی فیثاغورث و همچنین تئوری علمی دانشمندان مسلمان مانند فارابی و دیگران در این زمینه مورد بررسی قرار میگیرد.
در این جلسه به صورت مفصلتر به کارهای فارابی و دیگر دانشمندان در زمینه تئوری موسیقی و همچنین ارائه تعریف ریاضی برای فواصل هارمونیک پرداخته میشود.
رنگ آمیزی گراف
سعیده احمدی
23 شهریور 1385
Graph theory would not be what is today if there had been no coloring problems
در این سمینار پس از آشنائی با یکی از انواع رنگ آمیزیهای گراف به نام رنگآمیزی Harmonious با هم سعی در پیدا کردن عدد رنگی این رنگآمیزی در چند گراف خاص خواهیم کرد. (عدد رنگی حداقل تعداد رنگی است که گراف بهوسیله آن رنگآمیزی میشود.) در پایان نیز اشارهای به چند رنگآمیزی دیگر و کاربرد رنگآمیزیها خواهد شد. لازم به ذکر است است، رنگآمیزیها میتوانند در کلیه مسائل بهینه سازی کاربرد داشته باشند.
ایدههای نو در روش غربال
محمد الهیاری
16 شهریور 1385
به غربال گفتم: شنیدهای؟
چشمها را باید شست،
جور دیگر باید دید
حالا به شما هم میگویم که چه شد…
من دروغ میگویم!
مقداد قاری
9 شهریور 1385
شاید نام کانتور نابغه غمگین و انقلابگر بزرگ ریاضی و راسل زیرک را شنیده باشید.
احتمالا با “نظریه مجموعهها” و “پارادوکس راسل” نیز آشنائید. اگر با این مفاهیم آشنا نیستید اصلا نگران نباشید، من شما را با دنیای عمیق نظریه مجموعهها و ارادوکس راسل آشنا خواهم کرد. عنوان این گفتگو (من دروغ میگویم) در ریاضی پارادوکسی به نام “پارادوکس راسل” ایجاد کرد. اما ریاضیدانان آنقدر باهوش هستند که اجازه ندهند پارادوکسی در ریاضی رخ دهد. قصد داریم راه حل رضایتبخش و زیبائی از این پارادوکس ارائه دهیم.
Internet measurment
کاوه سلامتیان
28 مرداد 1385
This talk will provide an introduction to Internet measurement and modeling. We will look at flows at the IP level (as defined by the 5-tuple) and at the level of network ingress-egress (origin-destination flows) such as are used in traffic matrix estimation.
We will also give a glance on behaviors modeling and to the emergence of new applications and behaviors over Internet
Fractals and Image Compression
پدرام پاد
2 شهریور 1385
Fractals is a geometrical object which has some self similarities; this is a rough definition of a geometrical object called fractal.
In this lecture we will introduce a very important family of fractals which are based on Banach Fixed point Theorem. At first we will have a discussion or real mathematical analysis which will overcome the mathematical dependencies of the lecture. And at the end we will have a brief discussion on IFS and PIFS and their application in image compression (i.e. the mathematical backgrounds of Fractal Image compression.)
نظریه متروید
الهام روشنبین
27 مرداد 1385
مترویدها اولین بار توسط ویتنی در سال 1935 در تلاش برای فراهم آوردن یک رفتار مجرد یکسان از وابستگی در جبر خطی و نظریه گراف معرفی شدند. نام متروید ساختاری مربوط به یک ماتریس را القا میکند. تعریف ویتنی تنوع شگفتانگیز از ساختارهای ترکیبیاتی را در برداشت. از این گذشته مترویدها به طور طبیعی در بهینه سازی ترکیبیاتی پدیدار میشوند، زیرا آنها دقیقا همان ساختارهای ترکیبیاتی هستند که الگوریتم حریصانه برای آن به نتیجه میرسد. در این سمینار به معرفی نظریه متروید پرداخته و برخی قضایای اساسی آن بیان میشود.
گنگ بودن مقادیر پلی لگاریتم
آقای فاتحی
18 مرداد 1385
در سال 1979 نیکیشین با استفاده از تقریب هرمیت-پاد نوع اول ثابت کرد در نقاط نزدیک به صفر با شرط خاصی مقادیر تابع پلیلگاریتم گنگ میباشد. ریووال در سال 2000 ثابت کرد که مجموعهی توابع پلیلگاریتم به ازای اعداد گویائی که قدرمطلق آنها کوچکتر از 1 میباشند، شامل بینهایت عدد مستقل خطی روی Q است. ما قصد داریم ضمن معرفی بعضی از توابع خاص مانند تابع گاما، تابع بتا و تابع فوقهندسی، بعضی از کاربردهای آن را در نظریه اعداد به خصوص در اثبات قضایای نیکیشین و ریووال بررسی کنیم.
مدل ریاضی اینترنت
امین صابری
5 مرداد 1385
در این سمینار آقای دکتر “امین صابری” استاد دانشگاه استنفورد به سخنرانی درباره “مدل ریاضی اینترنت” پرداختند. وی در این سخنرانی با اشاره به حل مسایل ریاضی با استفاده از برخی قانونها ماند گرافها، تاکید کردند که این قواعد ریاضی در شبکه جهانی اینترنت و امکانات مختلف آن کاربردهای بسیاری دارد.
دکتر صابری برخی از این کاربردها را در مسایل مربوط به توزیع شبکه اینترنت و شاهراههای آن به مانند یک گراف منظم دانست و گفت: با استفاده از این قواعد میتوان به بهبود توسعه این شبکه کمک کرد.
وی دیگر کاربردهای مدلهای ریاضی در شبکه اینترنت را در مسائلی مانند تجارت الکترونیک و امنیت اطلاعات عنوان کرد و اظهار داشت: دانشمندان بزرگی از دهه 90 به بعد و با پیدایش شبکه اینترنت و گسترش آن به مساله مدل ریاضی اینترنت توجه ویژهای داشتهاند. گفتنی است آقای دکتر صابری به مدت یکسال با شرکت مایکروسافت در زمینه مدل ریاضی اینترنت همکاری داشتهاند.